摘 要 肯尼亞OLKARI地區(qū)地?zé)峋貙訙囟雀哌_(dá)
關(guān)鍵詞 泡沫鉆井 鉆井液 超高溫 實(shí)驗(yàn)研究 井筒壓力 計(jì)算方法 肯尼亞 0LKARI地區(qū) 地?zé)峋?span lang="EN-US">
泡沫鉆井液具有較高的攜巖能力,能夠有效地保持井眼清潔、提高鉆速。OLKARI地區(qū)地層異常高溫,有些地層的溫度可達(dá)
在以往的泡沫鉆井流體的研究中,未曾遇到過類似于肯尼亞地區(qū)的超高溫地層,泡沫都被簡(jiǎn)化成為氣液比穩(wěn)定、氣相液相無(wú)滑脫的模型,未考慮泡沫流體在井筒中的相態(tài)變化對(duì)鉆井參數(shù)計(jì)算準(zhǔn)確性的影響,現(xiàn)有的研究?jī)?nèi)容,已經(jīng)不能為超高溫地?zé)峋菽@井措施的改進(jìn)提供可靠依據(jù)。為此,有必要考慮超高溫對(duì)泡沫相態(tài)的影響,研究泡沫鉆井過程中井筒流體的相態(tài)分布,并改進(jìn)鉆井參數(shù)計(jì)算方法。
1地?zé)峋販胤植继攸c(diǎn)
OLKARI地區(qū)地?zé)峋牡販刈兓瘶O其異常,有的井深只有幾百米,地層溫度可超過
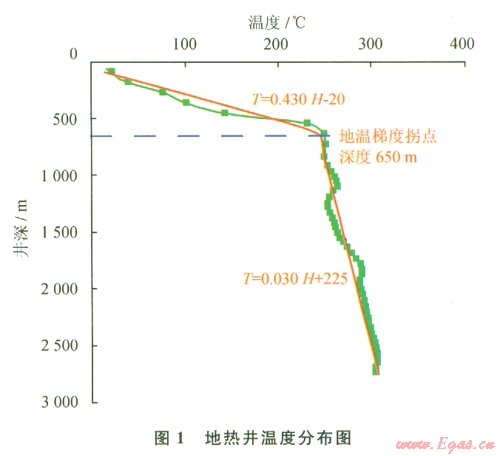
如圖l所示,根據(jù)該地區(qū)某井實(shí)測(cè)地溫?cái)?shù)據(jù)擬合結(jié)果,將地?zé)峋貙拥販靥荻群?jiǎn)化為0~
2泡沫基液相圖研究
研究泡沫的相變與單組分水的相變唯一的區(qū)別在于泡沫體系中含有空氣,即研究含水的真空容器中,空氣的引入對(duì)其相態(tài)變化的影響。忽略空氣在水中的溶解度。因此,該體系中液相為水,氣相為空氣和水蒸氣,兩者達(dá)到平衡。
對(duì)于空氣和水蒸氣組成的混合氣體,可以采用分壓定律來(lái)研究。由分壓定律可知,混合氣體形成的總壓等于空氣的分壓與水蒸氣的分壓之和,而各組分的分壓等于各組分所占的摩爾質(zhì)量分?jǐn)?shù)與該系統(tǒng)中氣相的總壓的乘積。

由于當(dāng)氣體中水的分壓小于當(dāng)前溫度、壓力條件下的飽和蒸氣壓時(shí),水即可蒸發(fā)。通過整理可得泡沫流體相變判別方程組:
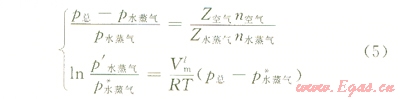
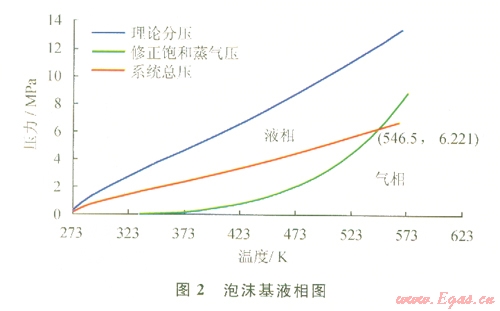
當(dāng)P水蒸氣大于P'水蒸氣時(shí),泡沫基液不會(huì)發(fā)生相變;當(dāng)P水蒸氣小于P'水蒸氣時(shí),泡沫基液會(huì)發(fā)生相變;兩者相等時(shí),即為相變分界點(diǎn)。
根據(jù)以上的分析可得到泡沫基液相圖(圖2)。從圖2可知,當(dāng)系統(tǒng)溫度到達(dá)546.5 K,壓力達(dá)到6.221 MPa時(shí),理論分壓線與修正飽和蒸氣壓線相交,即該交點(diǎn)為此系統(tǒng)發(fā)生相變的分界點(diǎn),低于該點(diǎn)的系統(tǒng)溫度和壓力,泡沫流體不會(huì)發(fā)生相變,高于該點(diǎn)的系統(tǒng)溫度和壓力,泡沫流體發(fā)生相變。
3 井筒內(nèi)流體壓力計(jì)算模型
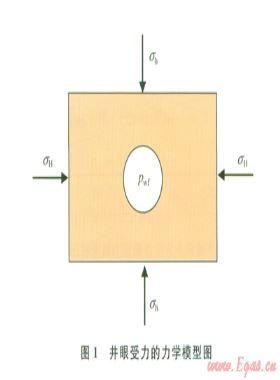
井筒內(nèi)壓力分布情況直接影響著井內(nèi)流體相態(tài)變化的情況。因此,就所涉及的流體流動(dòng)模型進(jìn)行介紹。
3.1氣體鉆井模型
3.1.1 氣體井內(nèi)流動(dòng)基本假設(shè)
為了對(duì)氣體鉆井時(shí)井內(nèi)流動(dòng)進(jìn)行較為準(zhǔn)確的描述,作如下假設(shè):①氣體在井內(nèi)作一維流動(dòng),因?yàn)榫畠?nèi)流道面積大大小于流道的縱向尺寸。因此,可以忽略流動(dòng)參數(shù)在徑向上的變化,井內(nèi)氣體流動(dòng)可按一維考慮。②井內(nèi)流動(dòng)溫度根據(jù)地溫梯度計(jì)算,Mitchell R.F[1]的計(jì)算結(jié)果表明,氣體鉆井過程中,流體處于完全非穩(wěn)態(tài)熱力學(xué)平衡時(shí),井內(nèi)流體溫度與地層溫度相近。因此,井內(nèi)氣體溫度可以根據(jù)地溫梯度求取。③井內(nèi)流動(dòng)為擬單相流動(dòng),氣體鉆井流體中,固相濃度較低。因此,將氣體鉆井流體的流動(dòng)視為單相流動(dòng),巖屑和干:粉僅對(duì)氣體的流動(dòng)壓力有影響。
3.1.2 氣體井內(nèi)流動(dòng)計(jì)算
3.1.2.1流動(dòng)計(jì)算的基本理論
1)鉆柱中氣體流動(dòng)方程。根據(jù)流體力學(xué)基本理論,氣體在鉆桿中流動(dòng)遵循的流動(dòng)方程為:
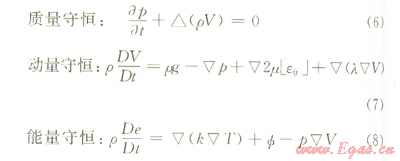
式中g為重力加速度;μ=μ(p、T)為黏性系數(shù);λ=λ(p、T)為體膨脹黏性系數(shù);k=k(p、T)為熱傳導(dǎo)系數(shù)。
2)環(huán)空中氣體流動(dòng)方程組。穩(wěn)定流動(dòng)方程:
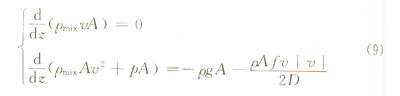
3.1.2.2鉆柱內(nèi)計(jì)算
立管壓力是指鉆井中立管處的壓力,鉆井中,氣體從立管進(jìn)入鉆桿,經(jīng)鉆頭后,沿環(huán)空返出地面。因此,立管壓力為井底壓力與鉆桿壓耗的之和。
根據(jù)鉆桿中氣體流動(dòng)方程組,在忽略等直徑微元段內(nèi)氣體流速變化的基礎(chǔ)上,可得壓耗為:
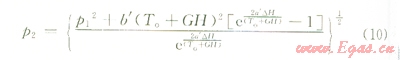
式中p1為微元段上游壓力,Pa;P2為微元段下游壓力,Pa;△H為微元段長(zhǎng)度,m。
3.1.2.3鉆頭流動(dòng)計(jì)算
氣體通過鉆頭水眼時(shí),流道面積突然擴(kuò)大,將產(chǎn)生較大的壓力損失,氣流速度增加,同時(shí)引起溫度的變化。即:
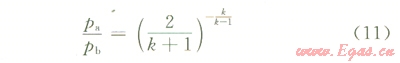
式中pb為下游壓力,Pa;pa為音速流動(dòng)時(shí)上游壓力,Pa;k為氣體比熱容。
3.1.2.4環(huán)空流動(dòng)計(jì)算
由環(huán)空氣體流動(dòng)方程組可知,對(duì)于等直徑的環(huán)空微元段,假設(shè)其中氣體流速不變,則由動(dòng)量守恒方程可得
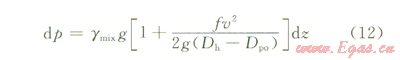
式中Dh為井眼尺寸,m;Dpo為鉆柱外徑,m;f為摩擦系數(shù);υ為流體返速,m/s;γmix為混合物重度,N/m3。
3.2泡沫鉆井模型
3.2.1泡沫鉆井基本假設(shè)
泡沫鉆井時(shí),井內(nèi)的流動(dòng)通道與氣體鉆井時(shí)相似。因此,二者可以采用相同的物理模型。為了便于對(duì)井內(nèi)泡沫的流動(dòng)規(guī)律進(jìn)行研究,需作如下假設(shè):①因井內(nèi)流道橫截面尺寸遠(yuǎn)小于縱向尺寸,故井內(nèi)泡沫流動(dòng)考慮為一維流動(dòng);②注入井內(nèi)的泡沫在地面已經(jīng)充分發(fā)泡,在井內(nèi)的各個(gè)位置,流體都以泡沫形式存在;③泡沫是一種高黏度流體,氣相和液相之間無(wú)滑脫,兩相的相速度相同;④泡沫氣液相間無(wú)化學(xué)反應(yīng),且相間沒有質(zhì)量交換,只有能量交換;⑤泡沫流體溫度由地溫梯度或?qū)崪y(cè)數(shù)據(jù)確定。
3.2.2泡沫鉆井流體計(jì)算
3.2.2.1井內(nèi)泡沫流體基本理論
1)連續(xù)性方程
氣相連續(xù)方程:

式中μe為泡沫的有效黏度,Pa·s,其值與泡沫質(zhì)量有關(guān).由泡沫流變模型決定;ρm為泡沫密度,kg/m3,ρm=ρgɑg +ρ1ɑ1;υ為泡沫流動(dòng)速度,m/s;D為流道當(dāng)量直徑,m;fF為泡沫受到的摩擦阻力系數(shù),由泡沫流動(dòng)雷諾數(shù)確定[2-3]。
3.2.2.2井內(nèi)泡沫流動(dòng)的計(jì)算
穩(wěn)定流動(dòng)時(shí)流動(dòng)參數(shù)不隨時(shí)間變化,氣體在井內(nèi)穩(wěn)定流模型為:
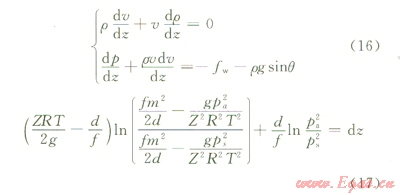
上式就是控制體內(nèi)氣體流動(dòng)的上下段的壓力關(guān)系,其中pa為上游壓力,ps為下游壓力,dz為控制體長(zhǎng)度,當(dāng)給定下游壓力,計(jì)算控制體上游壓力pa1再以pa1下游壓力計(jì)算上游壓力(pa2),沿劃定網(wǎng)格迭代計(jì)算,直到計(jì)算處立管壓力(ps)。
3.2.2.3鉆頭泡沫流動(dòng)的計(jì)算
噴嘴處泡沫流動(dòng)可作如下假設(shè):①泡沫處于穩(wěn)定流動(dòng)狀態(tài);②忽略因噴嘴高度變化引起的重位壓差;③泡沫在噴嘴中作等熵流動(dòng)。
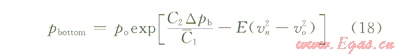
式中pbottom為井底壓力,Pa;po為噴嘴上游壓力,Pa;υn、υo分別為噴嘴出口、進(jìn)口流速,m/s;△pb為鉆頭噴嘴處的壓力降,Pa,且有:
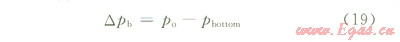
4 井筒內(nèi)流體相態(tài)分析
井筒內(nèi)流體相態(tài)分析主要在前人研究基礎(chǔ)上,通過理論分析與經(jīng)驗(yàn)結(jié)合的方式,著重分析泡沫相態(tài)變化對(duì)鉆井液在井筒中所處流型的影響,推導(dǎo)出更為接近存在相態(tài)變化的泡沫鉆井實(shí)際工況的計(jì)算方法。
4.1 井筒耦合流動(dòng)計(jì)算方法
首先判斷出當(dāng)前位置泡沫基液是何種相態(tài),有無(wú)發(fā)生相變,然后判定相變后鉆井液所處的流型,根據(jù)不同位置鉆井液所處的不同流型選擇不同的動(dòng)力參數(shù)計(jì)算模型,從而得出泡沫鉆井的關(guān)鍵參數(shù)。求解計(jì)算模型步驟如下:
1)以井口壓力為起點(diǎn)[4],按照深度對(duì)井筒環(huán)空進(jìn)行離散處理,內(nèi)層循環(huán)用于計(jì)算各個(gè)節(jié)點(diǎn)單元的壓降,外層循環(huán)用于計(jì)算溫度。在開始計(jì)算的時(shí)候必須知道以下參數(shù):穩(wěn)態(tài)流動(dòng)的氣液流量、密度、黏度,井口回壓,井身結(jié)構(gòu)和鉆具組合幾何尺寸,軌跡數(shù)據(jù),井口溫度,地溫梯度,管子內(nèi)外壁粗糙度等。
2)根據(jù)地溫梯度計(jì)算離散單元的溫度增量和節(jié)點(diǎn)溫度Ti0。
3)假設(shè)該離散單元的壓降△po,并計(jì)算該單元的平均溫度和平均壓力。
4)在平均壓力溫度下計(jì)算氣液物性參數(shù):環(huán)空質(zhì)量數(shù)、表觀黏度、混合物密度、液相黏度、環(huán)空返速、巖屑沉降速度、傳輸比、巖屑濃度、氣液界面張力等。
5)進(jìn)行泡沫兩相流特性參數(shù)計(jì)算。
6)判斷計(jì)算的離散單元壓耗和假設(shè)壓耗是否滿足精度要求,不滿足就返回第4步計(jì)算,否則進(jìn)行下一步計(jì)算。
7)應(yīng)用井筒傳熱方程和能量方程計(jì)算離散單元節(jié)點(diǎn)溫度。
8)判斷計(jì)算的離散單元溫度和假設(shè)溫度是否滿足精度要求,不滿足就返回第4步計(jì)算,否則進(jìn)行下一步計(jì)算。
9)應(yīng)用本文提到的泡沫基液相圖,判斷鉆井液是否發(fā)生相變,如果沒有發(fā)生相變,繼續(xù)計(jì)算下一離散單元,否則選擇氣體鉆井理論模型返回第4步重新計(jì)算該離散單元,如此循環(huán)計(jì)算出泡沫鉆井的井筒壓力剖面。
4.2井筒內(nèi)流體相態(tài)分布規(guī)律
下面將根據(jù)井筒耦合流動(dòng)計(jì)算方法,以OLKARI地區(qū)某超高溫地?zé)峋疄槔M(jìn)行井筒流體相態(tài)分析。泡沫基液的相態(tài)變化規(guī)律如圖3。
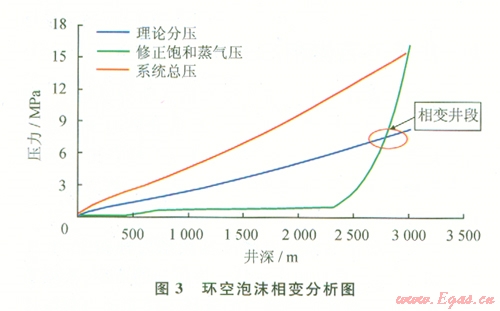
由圖3分析可得到以下結(jié)論,泡沫鉆井液在環(huán)空2
5 結(jié)論
筆者針對(duì)超高溫地?zé)峋@井技術(shù)難題,通過對(duì)穩(wěn)定泡沫鉆井理論模型研究以及氣體鉆井理論模型研究,最終形成了一套適用于地?zé)徙@井的高溫泡沫相變耦合流動(dòng)計(jì)算模型,同時(shí)進(jìn)行了現(xiàn)場(chǎng)實(shí)例計(jì)算,取得以下幾點(diǎn)結(jié)論與認(rèn)識(shí)。
1)在鉆進(jìn)過程中,如果泡沫流體相態(tài)發(fā)生變化,其密度等參數(shù)將發(fā)生變化,直接影響井底壓力的推算,并且導(dǎo)致井筒流體流態(tài)及工況參數(shù)改變,可能導(dǎo)致井下復(fù)雜情況的出現(xiàn)。
2)通過對(duì)相變基本理論進(jìn)行研究,基于分壓理論,同時(shí)考慮惰性氣體對(duì)液相飽和蒸氣壓的影響,建立了泡沫流體相變判別模型,并針對(duì)不同壓力、溫度條件下的泡沫流體進(jìn)行了相變分析,當(dāng)某溫度壓力下的理論分壓低于該溫度壓力下的修正飽和蒸氣壓時(shí),泡沫流體發(fā)生相變。
3)基于氣基流體多相流理淪,建立了井下穩(wěn)定泡沫鉆井理論模型和氣體鉆井理論模型。并將泡沫基液相變判別模型、穩(wěn)定泡沫鉆井理論模型以及氣體鉆井理論模型相耦合,最終形成了一套適用于地?zé)徙@井的高溫泡沫相變耦合流動(dòng)計(jì)算模型。
4)運(yùn)用OLKARI地區(qū)某超高溫地?zé)峋膶?shí)際資料進(jìn)行了實(shí)例計(jì)算。結(jié)合高溫泡沫相變耦合流動(dòng)模型進(jìn)行分析,可以更準(zhǔn)確地了解工作液的工作狀態(tài),為高溫地?zé)徙@井安全鉆進(jìn)提供了科學(xué)依據(jù)。
參 考 文 獻(xiàn)
[1] MITCHELL R F.Simulation of air and mist drilling of geothermal wells[J].Journal of Petroleum Technology,1983,35(11):2020-2126.
[2] TAN H C S,MCGOWN J M,MCGO J M.Friction pressure correlation for C02 foam fluids[C]//paper 21856-MS presented at the Low Permeability Reservoirs Symposium,15-17 April l991,Denver,Colorado,USA.New York:SPE 1991.
[3] LIU Gefei,MEDLEY G H Jr.Foam computer model helps in analysis of underbalanced drilling[J].Oil & Gas Journal.1996,94(27):114-119.
[4] 樊世忠,余金海.泡沫流體鉆井技術(shù)[M].北京:石油工業(yè)出版社,1991.
本文作者:王文勇 龍俊西 劉博偉 李皋 孟英峰
作者單位: “油氣藏地質(zhì)及開發(fā)工程”國(guó)家重點(diǎn)實(shí)驗(yàn)室·西南石油大學(xué) 中國(guó)石油長(zhǎng)城鉆探工程有限公司國(guó)際鉆井公司
您可以選擇一種方式贊助本站

支付寶轉(zhuǎn)賬贊助

微信轉(zhuǎn)賬贊助