摘要:隨著地震勘探進入四川盆地周邊大山區以及盆地內低、降速帶極其嚴重的復雜近地表區,即便是采用最佳擬合的浮動基準面來處理,其剩余動校正量也足以破壞淺、中層數據疊加成像。研究動校時差理論發現,動校正量客觀地存在于野外采集記錄中,它不僅與炮檢距有關,而且還與近地表、地下速度結構緊密相關,而與地表一致性靜校正結果則無關。因此,動、靜校正應該是相互獨立而有序的兩件事,不應該把兩者混在一起,更不應該先作靜校正、后作動校正。這是近些年來在研究浮動基準面所沒有觸及的實質性問題。為此,在分析大山區復雜近地表數據受剩余動校正量的實際影響之后,提出了把動、靜校正分開,先作動校正、后作靜校正處理,視浮動基準面為靜校正中一個概念的一套真地表動校疊加技術。該技術方案既適應復雜近地表情況,又滿足了各種復雜條件的要求,處理的地震資料淺、中層成像普遍得到改善,也更符合實際地質情況,為后續的深度偏移處理打下了基礎。
關鍵詞:真地表;動校正;剩余動校正量;浮動基準面;地震資料處理;四川盆地
1 復雜近地表區對浮動基準面技術的挑戰
本文參考文獻[1]中大量的計算證明,在地形起伏比較小時,以炮、檢中點為基準線作靜校正,則校正誤差最小。這實際上是指動校正的參考點選在炮、檢中點位置,即相當于動校正曲線的零點和實際記錄的時間零點相匹配,則剩余動校正量等于零,這就是浮動基準面的雛形。后來,在排列長度比較小時,地形起伏也不大,動校正的參考面(即浮動基準面)都是用一個排列長度作為平滑參數(即1個CMP道集1個炮、檢點靜值平均值,該值與道集內各道炮、檢點靜值的差值作為相對靜值)產生的(圖1)。自20世紀80年代中期創建浮動基準面以來,在一般小山區、丘陵地區、高差不是很大、且排列也不是很大情況下,浮動基準面條件下的相對靜值一般表現為高頻成分。這符合最小靜值準則,對動校正沒有多大影響。而盆地周邊大山區的特點是:地形相對高差大、起伏頻度大,再加上排列不斷增大,相對靜值中包含大量的中、低頻成分,這就不能滿足最小靜值準則,使動校正量有過量的剩余,浮動基準面技術就顯現出局限性了。對平原及沿海灘涂,低、降速帶突出,相對靜值也不會只有高頻成分,甚至包含有大的低頻成分,先做相對靜校正也會影響動校正的正常規律。
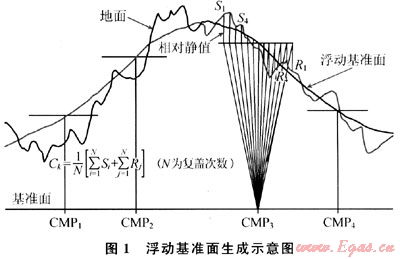
1.1 實例分析
選擇了川西大山區、川中小山區和類似川西平壩的印尼海邊測線,展示了它們的近地表結構、某些點的浮動基準面值及高程和層析靜值差值分布,以期尋找到一些規律。
川西大山區某線CMP2250道集中炮、檢中點分布,排列長度最大7200m。該線展示了大排列、大的地形起伏下(相對高差大于1000m)有大的炮、檢中點離散度,約為260ms(雙程時間)。計算浮動基準面時,若按最小半徑平滑,其值為175ms,按最大半徑平滑為140ms。最大最小平滑結果相差雙程時間70ms。依據最佳擬合原則作平滑,最終所選的CMP基準面值為160ms,基本上處于各炮、檢中點分布的重心位置,從而使近80%的道處于80ms誤差范圍內。
川中LG3D的1個CMP點的炮、檢中點分布中,其離散度達±60ms。該區地形較平坦的二維某線,最大炮檢距只有1890m,離散度達±40ms。
地形相當平坦的沿海某線,最大炮檢距2625m,炮、檢中點最大離散度達±50ms。其高差和層析靜值的差值曲線則表現出相當大的長、短波長靜值變化,說明該區近地表結構縱、橫向變化很大。
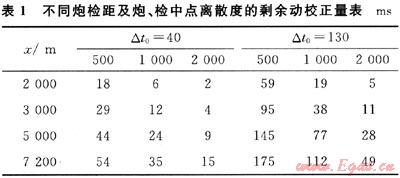
在某些條件下,這樣大的離散度也是不可容忍的。如圖2所示:當地形有起伏、處理基準面為水平基準面時,先作靜校正,相當于把動校正的參考點放在水平基準面上,動校正曲線相對實際記錄道作了△t0的時移,使地震記錄作動校正后產生了剩余動校正量。這個剩余動校正量是隨著深度的增加而變小,隨著炮檢距的增大而變大,從而有了所謂的“靜校不靜”問題。表1為炮、檢中點離散度(△t0)對不同炮檢距(x)和反射時間(t0)的剩余動校正量表。這里取其下限,使用較高速度(v=5000m/s)做常規動校正計算。從表1可以看出,通常情況下(大山區、5000m以上炮檢距)可影響到2s數據成像。
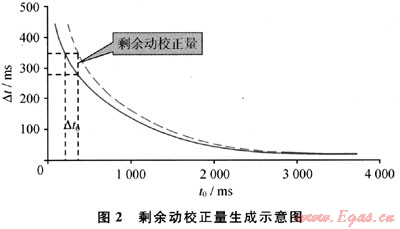
1.2 理論分析
1.2.1一般傾角時差校正方程
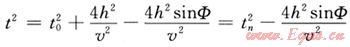
其中tn2=t02+4h2/v2
式中t0為反射時間;v為速度;Φ為傾角;h為炮檢距。
可見動校正規律不僅與炮檢距有關,而且還與速度結構(t0、v、Φ)緊密相關。
地質體的速度結構是最終要求解的,只有近地表速度結構才是影響靜校正的因素[2]。近年來,靜校正技術的發展使其能用比較精確的方法獲得了近地表結構。因此,原始記錄的時間就是有效反射波從地面到地下反射界面,經復雜地質體,又經目前計算的近地表結構,在地表被接收器接收的時間。所以,在作動校正時這個時間是不能隨便改變的。也就是說,動校正量客觀地存在于野外所采集的地震記錄中,它與近地表及地下速度結構相關,或稱為與近地表及地下的非均質性相關(當然與炮檢距相關聯),而與地表一致性的靜校正結果無關。
因此,動校正、靜校正應該是相互獨立而有序的兩件事。不應該將二者混在一起,更不應該先靜校正、后動校正。這是多年來沒有研究人員關心的一件事。
1.2.2關于最小靜值準則
1) 最小靜值準則就是動校前的靜校正量應該最小,不要去破壞記錄本身的動校正規律。使得動校正誤差最小,但不是沒有[3]。
2) 從速度分析的角度講,速度分析必須用一個排列范圍內的道掃描速度。排列越大則動校正量越大,速度的分辨率越高,一個地區應該有一個較大的排列長度。但排列增大,平滑程度加大,浮動基準面就更平緩(圖1)。對大山區以及低、降速帶嚴重地區,相對靜值是相當大的,這和最小靜值準則相違背。
3) 更為關心的是速度的起點,或叫速度的時間坐標是否和記錄的時間坐標相一致。最小靜值準則就是講二者誤差問題。
4) 對于高陡復雜構造,陡傾角需要大炮檢距。但是,大炮檢距又增大了浮動基準面的平滑程度,使相對靜值中富含中、低頻成分。這樣,二者誤差更大。
1.2.3小結
以上分析表明:目前常規CMP基準面下,不管是大山區還是低、降速帶嚴重的沿海灘涂,由于浮動基準面使相對靜值的離散度很大,致使剩余動校正量很大;在資料的常規處理中,都是先靜校正,后動校正,從而破壞了原始記錄的動校正規律,使動校正中的理論曲線與實際記錄時間不匹配。因此,能否找到一個既適合各種復雜情況、又能滿足各種復雜條件要求的完全方案呢?
2 各種動校疊加方法研究現狀
2.1 常規浮動基準面動校疊加方法
2.1.1炮、檢點的相對時移量
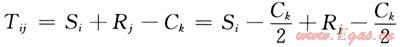
式中Si和Rj為炮、檢點靜校正量;Ck為炮、檢中點k位置上道集內平均時移(低頻的CMP基準面值)。
2.1.2動校正量表達式
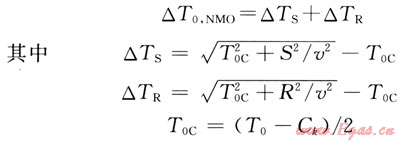
式中△TS和△TR為炮、檢點正常時差;S、R為炮點和檢波點到CMP點水平距離;口為動校正速度;T0C為CMP點的丁T0時間;T0為基準面時間。
2.1.3效果
當地形起伏頻度大、相對高差大、排列大(炮檢距大)或低、降速帶(厚度、速度)的縱橫向變化大時,Ck面(CMP基準面)常常遠離地面,從而造成△T0.NMO有很大誤差(剩余動校正量)。
2.2 原有的真實地表動校正方法[4]
2.2.1動校正量表達式

式中D、Zi和Zj分別為基準面、炮點和檢波點高程;vr為替換速度。
2.2.2效果
用替換速度把炮、檢點高程換算為時間,這個時間并不等于記錄地震波所經歷的時間。因此,動校正并沒有從真實地表開始,還有剩余動校正量存在。
盡管沒有設浮動基準面,實際上已經很接近以每道炮、檢中點為參考點作動校正。其剩余動校正量較小,所以效果較好。
2.3 最小靜校正誤差浮動基準面方法[5]
2.3.1方法
1) 本文參考文獻[5]證明,當浮動基準面在地面和低速帶底板之間時(即hd=hd0-△hd,hd0和hd為地面和浮動基準面高程,△hd為浮動基準面與地面之差值)靜校正誤差最小(其靜值均方誤差在平滑地面、高速面、平均靜值面之中是最小的)。
同時,從本文參考文獻[5]還可以看出:v2/v1越大,則△hd越大(v1為低速帶速度,v2高速層速度);x越大,則△hd越大(x為炮檢距)。
2.3.2條件
x<1000m,v2/v1比較小,△h<400m(△h為相對高差)。
2.3.3效果
△hd越大,則動校正越不遵循地震波射線傳播規律,剩余動校正量越大。
以上條件都是比較簡單的近地表條件。對大山區、沿海灘涂等復雜近地表條件則不適合。
即便在以上簡單條件下,也是丟棄動校正誤差影響、強調疊加速度應取決于低速帶底板速度為標準,在地面和高速層之間尋找的折中方案。
3 真地表動校疊加技術
以上方法各有千秋。相比之下,第2種方法效果較好,但也有不足:①不該用替換速度校正炮、檢點高程作為動校正的起點,這樣就主觀地改變了炮點和檢波點的相對位置;②不設浮動基準面就無法掃描疊加速度。
顯然,以上方法都沒有考慮從根本上解決剩余動校正量問題。真地表動校疊加技術將以一種新的思路彌補了以上各方法的不足。
3.1 動校正公式
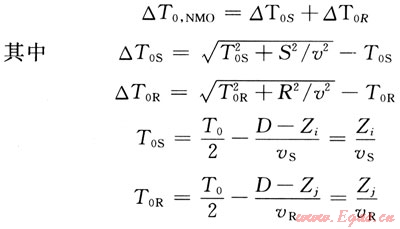
式中vS和vR為炮、檢點的速度函數。
3.2 建立浮動基準面(與常規相同)
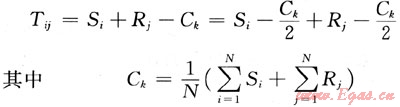
式中N為覆蓋次數。
3.3 新方案的特點
1) 該方案與第2種方法的區別在于動校正參考點放在了真正的地面,從而使動校正嚴格地遵循了地震波射線的傳播規律。
2) 在處理流程中嚴格地將動、靜校正分開,按先動校正、后靜校正的原則進行速度分析、動校和疊加。
3) 真地表也不是以地表為浮動基準面,浮動基準面應該是靜校正中的一個概念。
4) 如果一定要說動校正有浮動基準面的話,那就是以每道炮、檢中點為參考的一個虛擬的面。
5) 這里不存在(也不需要)最小靜值準則概念。
6) 顯然,該技術不受最大炮檢距的限制,同時也為大炮檢距的一套處理方法掃清了障礙。
4 新方案下的效果分析
4.1 剩余靜校正量更加地表一致性化
由于動校正嚴格地遵循了地震波射線的傳播規律,這里不存在最小靜值準則,也就不存在剩余動校正量。因此,剩余靜校正過程中也就沒有剩余動校正量的干擾,剩余靜校正量更加地表一致性化。與常規剖面相比,淺、中層資料成像普遍得到改善(圖3、4)。
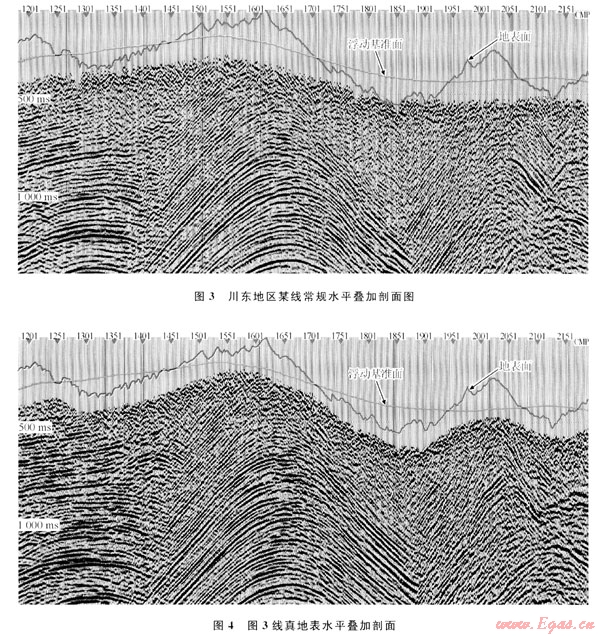
4.2 關于最大炮檢距
新的動校正方案將不限制炮檢距。一個地區無論排列(最大炮檢距)多么大、近地表條件多么復雜,從而使相對靜值再大也影響不到動校正。在設計排列長度時,至少缺了一個可顧及的因素。同時,也為大炮檢距的一套處理方法(如視各向異性)掃清了障礙(去掉了剩余動校正量的干擾)。
4.3 關于動校正誤差
動校正的誤差將不再來自于相對靜值離散度大的干擾。現在的動校誤差僅取決于速度的準確度,以及由近地表模型所計算靜值的誤差。盡管資料經自動剩余靜校正后速度和剖面質量都有很大提高,但是目前的疊加速度都是由人工選取的,由于認識和成像技術的多解性,使誤差在所難免。
4.4 浮動基準面的功能
現在的浮動基準面僅是靜校正中的一個概念,是速度分析的一個重要工具。因為靜值的長、短波長是由排列長度定義的,所以它是長、短波長靜值的一個分界線。
新方案下動校正的參考點是地面,但真地表并不是以地表為浮動基準面,它是以每道炮、檢中點為參考的一個虛擬的面。該面和靜校正中的浮動基準面有差異,一般情況下該差異表現為高頻成分,最終該差異將反映在所選的速度中。因此,新方案所選速度淺層普遍降低,但是現在的速度與介質速度更有關聯度,與層析模型的淺層具有一致性。
4.5 關于疊加速度
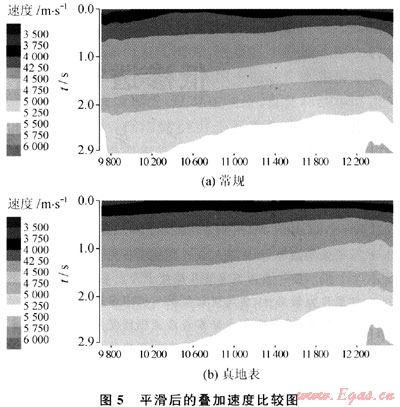
目前的疊加速度將受近地表淺層低速帶的影響。對習慣于用疊加速度作偏移,甚至用疊加速度作時一深轉換的做法可能認為不妥,只需將速度作個基準面校正或以一定長度的平滑濾波,去掉高頻成分,還是可以應用的(圖5)。但這都是在一般比較平緩構造下的情況,在高陡復雜構造情況下,還是要先作DM0,經DM0后所掃速度才能為偏移和時深轉換提供比較合理的速度。從圖5-b可看出,淺層層次感更清楚、橫向更穩定。
5 結束語
自20世紀80年代創建浮動基準面以來,從來都把動校正零點放在浮動基準面上。早期,受地震勘探區域限制(工作在平原或小丘陵區,排列比較小)用排列長度平滑所建浮動基準面和地面很接近,從而使動校正誤差比較小,也就沒有引起重視。嚴格地講,只要有地形起伏,有低、降速帶存在,用排列長度(最大炮檢距)平滑生成浮動基準面就會有相對靜值存在。把動校正零點放在浮動基準面上,就一定有剩余動校正量存在。
所以,真地表動校疊加技術具有普遍意義。但老的方案也不是特例,而是早期勘探階段認識不到位的一個臨時辦法。因為特例是指野外沒有地形起伏,其近地表為均質情況,在這種情況下也就不需要浮動基準面了。
參考文獻
[1] 周彬忠,包吉山.山區靜校正問題分析[J].石油地球物理勘探,1985,20(6):581-596.
[2] 王進海,唐怡,朱敏,等.復雜近地表結構的再認識[J].天然氣工業,2009,29(11):30-33.
[3] 胡英,張研,陳立康,等.速度建模的影響因素與技術對策[J].石油物探,2006,45(5):503-507.
[4] 王有新.復雜地表情況的動校方案[J].石油地球物理勘探,2002,37(2):105-108.
[5] 林伯香.最小靜校正誤差浮動基準面方法[J].石油地球物理勘探,2003,38(6):611-617.
(本文作者:王進海 梁波 朱敏 齊俊寧 李登亮 川慶鉆探工程有限公司地球物理勘探公司)
贊 賞 分享
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助
- 注解:本資料由會員及群友提供僅供閱讀交流學習,不得用于商業用途!
