摘 要 由于天然氣水合物特殊的理化性質(zhì),水合物地層要比常規(guī)地層的井壁穩(wěn)定問題更加復(fù)雜,鉆井液溫度對天然氣水合物地層的穩(wěn)定性影響將是一個不容忽視的因素。為此,考慮熱傳導(dǎo)、對流、水合物分解、地層力學(xué)性質(zhì)變化等諸多因素及其相互耦合作用,建立了溫度影響天然氣水合物地層井壁穩(wěn)定的數(shù)學(xué)模型,并進(jìn)行有限元求解。最后以國外某深水天然氣水合物地層實際取得的地質(zhì)資料為例,計算分析了鉆井液溫度對地層水合物分解、地層力學(xué)性質(zhì)變化及井壁穩(wěn)定的影響規(guī)律。結(jié)果表明:地層水合物因受熱分解會導(dǎo)致地層力學(xué)性質(zhì)急劇變差,進(jìn)而極易導(dǎo)致地層屈服失穩(wěn),選擇低溫體系鉆井液并控制其溫度低于水合物相平衡溫度,有助于維持井壁穩(wěn)定,實現(xiàn)安全鉆進(jìn)。
關(guān)鍵詞 天然氣水合物地層 鉆井液 溫度 井壁穩(wěn)定模型 有限元模擬 地層屈服失穩(wěn) 相平衡溫度
自然界的天然氣水合物(以下簡稱水合物)廣泛分布于深水海底、陸地永凍土帶和一些內(nèi)陸湖的深水沉積物中[1-2]。在水合物開采或深水區(qū)域油氣鉆探過程中,水合物地層被打開后,由于鉆井液的溫度要高于水合物地層溫度,水合物穩(wěn)定存在的相平衡條件被破壞而極易發(fā)生水合物分解,進(jìn)而導(dǎo)致地層力學(xué)性質(zhì)變差,對井壁穩(wěn)定帶來極大的不利影響,直接關(guān)系到鉆井的成敗與成本的高低。國內(nèi)外對水合物地層的井壁穩(wěn)定研究還在起步階段,并且沒有實際的經(jīng)驗積累,因此通過模擬的手段對該問題進(jìn)行研究將具有重要意義。
目前國內(nèi)外關(guān)于鉆井液溫度對水合物地層井壁穩(wěn)定影響的研究主要有室內(nèi)實驗和數(shù)值模擬兩種手段。實驗研究多是考慮溫度對水合物層的傳熱及其引起的水合物分解的分析,沒有從力學(xué)性質(zhì)的角度來研究井壁穩(wěn)定的問題[3-5];數(shù)值模擬研究往往沒有全面考慮溫度的影響機(jī)制,對地層孔隙中氣、水及水合物對導(dǎo)熱性質(zhì)的變化考慮不足[6-7]。在綜合考慮熱傳導(dǎo)、對流及水合物分解吸熱等因素的條件下,建立水合物地層能量守恒方程,同時考慮水合物分解動力學(xué)、地層流體滲流、井眼附近應(yīng)力狀態(tài)及力學(xué)性質(zhì)變化,并考慮這些因素問的互相耦合作用,通過有限元模擬的方法來研究鉆井液溫度對水合物地層井壁穩(wěn)定的影響。
1數(shù)學(xué)模型的建立
1.1 水合物地層能量守恒方程
在考慮熱傳導(dǎo)、對流、外界能量補(bǔ)給,以及水合物分解吸熱等因素的條件下,忽略動能和熱輻射,并忽略氣體的節(jié)流效應(yīng)和壓力對水及水合物熱焓的影響,能量守恒方程采用熱焓和溫度的形式表示為:

式中φ為孔隙度;ρ為密度,kg/m3;H為熱焓,J/kg;S為飽和度;ν為流速,m/s;Cp為比熱,J/(kg·K);下標(biāo)r、H、g和w分別代表巖石、水合物、氣體和水;Kc為地層有效熱傳導(dǎo)系數(shù),W/(m·K);Qin為外界的能量補(bǔ)給,J/(m3·s)。
式(1)左邊表示系統(tǒng)的內(nèi)能增量,等式右邊第一項表示通過熱傳導(dǎo)作用進(jìn)入單位多孔介質(zhì)系統(tǒng)的能量,等式右邊第二項表示外界對水合物地層的熱量補(bǔ)給,等式右邊第三項表示水合物分解所吸收的能量。
1.2 天然氣水合物分解動力學(xué)方程
采用Kim-Bishnoi天然氣水合物分解動力學(xué)模型[9]:

式中mg為單位體積地層天然氣的生成速率,kg/(m3·s);Mg為天然氣摩爾質(zhì)量;p為壓力,Pa;Φe、Φg分別為天然氣在pe和pg下的逸度系數(shù);Adec為單位體積地層內(nèi)水合物分解表面積,m-1;SH為水合物飽和度;Ahs為單位體積地層比表面積,m-1;Kd0為水合物本征分解速率常數(shù),mol/(m2·Pa·s);ΔE為反應(yīng)活化能,J/mol;對于甲烷水合物[8],Kd0等于8 060 mo1/(m2·Pa·s),ΔE等于77 330 J/tool;R為氣體常數(shù),8.314J/(mol·K);T為溫度,K。
1.3滲流方程
假定地層孔隙中含水、氣體和水合物三相,只有水和氣體兩相可以流動。基于連續(xù)性方程及廣義達(dá)西定律等,得到滲流方程:

式中Krg、Krw分別為氣和水相對滲透率;[K]為滲透率矩陣,m2;μg、μw分別為氣和水的黏度,Pa·s;qg、qw分別為氣、水源匯項,kg/(m3·s);g為重力加速度,m/s2;νs為巖石骨架運移速度,m/s;mw為單位體積地層內(nèi)水生成速率,kg/(m3·s);mH為單位體積地層內(nèi)水合物分解速率,kg/(m3·s);其他符號意義同前。
1.4應(yīng)力場方程
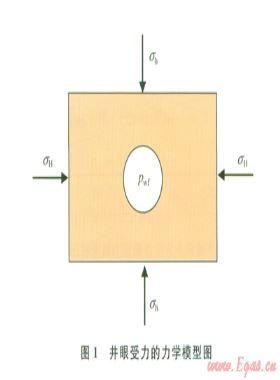
根據(jù)彈塑性力學(xué)理論,得到巖石骨架應(yīng)力場方程,基于有效應(yīng)力原理,平衡方程為: ’

式中σij為巖石骨架有效應(yīng)力,MPa;fi為體力載荷,MPa;ρi為孔隙壓力,MPa;a為Biot系數(shù);δij為Kronecker函數(shù)。
幾何方程的張量形式:

式中εij為應(yīng)變張量;u為位移。
采用彈塑性本構(gòu)方程及Drucker-Prager屈服準(zhǔn)則,本構(gòu)方程增量形式:

式中dσij為有效應(yīng)力增量;Dijkl為彈塑性矩陣張量;dεkl為應(yīng)變增量。
綜合以上水合物地層能量守恒方程、分解動力學(xué)方程、地層滲流方程和應(yīng)力場方程,再輔以相應(yīng)的輔助方程、初始和邊界條件,即構(gòu)成了完整的水合物地層井壁穩(wěn)定有限元分析數(shù)學(xué)模型。
2有限元模擬及結(jié)果分析
2.1物理模型及模擬所需參數(shù)
考慮簡化的二維平面應(yīng)變模型,幾何尺寸l

滲流場邊界條件:BC、CD兩邊為固定孔隙壓力邊界,AB、DE兩邊為自由邊界,AE井眼處為井底液壓邊界。
溫度場邊界條件:BC、CD兩邊為固定原始地層溫度邊界,AB、DE兩邊為自由邊界,AE井眼處為鉆井液溫度邊界。
巖石骨架應(yīng)力場邊界條件:BC、CD兩邊分別作用最大、最小有效水平地噓力,AE邊為有效井眠液槿壓力,AB邊為x向滑移邊界,DE邊為y向滑移邊界。
模型內(nèi)部分布有初始地層孔隙壓力、溫度和含水合物飽和度。
2.2鉆井液溫度對地層水合物分解的影響
鉆井液溫度為本研究的主要因素,取工況為平衡壓力鉆井,模擬水合物地層打開l h后不同鉆井液高于地層的溫度差時井壁附近地層的水合物分解情況,結(jié)果如圖2所示。可以看出,隨著鉆井液高于地層的溫度差越大,井壁附近的水合物分解范圍也越大,溫差為13 K時水合物分解范圍相對4 K時增大了l4.2%。1體積的水合物完全分解可產(chǎn)生164體積的氣體[11-12],這些氣體進(jìn)入井筒后將會帶來極大的風(fēng)險,鉆井液受到氣侵而密度將低,進(jìn)而導(dǎo)致鉆井液柱壓力降低,可能造成井壁的垮塌。

從井壁附近地層的溫度與水合物飽和度分布(圖3)可以看出,鉆井液溫度向地層傳播的范圍要大于水合物分解的范圍,說明地層中的水合物只有在溫度達(dá)到能夠破壞其相平衡的溫度時才會發(fā)生分解。控制鉆井液的溫度低于水合物的相平衡溫度,是水合物地層鉆井過程中重要的安全保證。

2.3 鉆并液溫度對地層力學(xué)性質(zhì)的影響
本節(jié)分析沿用前面分析的基本模型和條件,研究鉆井液溫度高于地層溫度時引起水合物分解對地層力學(xué)性質(zhì)影響。取地層彈性參數(shù)彈性模量和強(qiáng)度參數(shù)內(nèi)聚力來進(jìn)行分析,各自隨鉆井液高于地層的溫差變化情況如圖4、5所示。可見隨鉆井液溫度的升高,地層力學(xué)性質(zhì)變差的區(qū)域逐漸擴(kuò)大。

同時對比水合物飽和度分布圖(圖2),由于溫度升高引起水合物分解,導(dǎo)致地層彈性模量和內(nèi)聚力大幅降低,力學(xué)性質(zhì)變差。彈性模量由原始地層的6 375 MPa降為4 520 MPa左右,內(nèi)聚力由原始地層的2 MPa降為水合物分解后的1.5 MPa左右。從圖4還還可以看出,在距井眼中心0.2~0.
2.4鉆井液溫度對井壁穩(wěn)定的影響
約定地層屈服指數(shù)來表征地層的失穩(wěn)屈服情況,屈服指數(shù)等于l時地層為穩(wěn)定的,屈服指數(shù)小于l時地層發(fā)生屈服失穩(wěn),模擬得到不同鉆井液高于地層溫差時沿最小水平地應(yīng)力方向(沿ED邊)的屈服指數(shù)分布,如圖6所示。可見隨著鉆井液的溫度升高,地層失穩(wěn)屈服的區(qū)域增加。與水合物飽和度和地層力學(xué)性質(zhì)變化區(qū)域相對應(yīng),井壁附近地層水合物由于鉆井液的傳熱作用而發(fā)生分解,水合物對地層巖石顆粒的膠結(jié)作用減弱,導(dǎo)致地層力學(xué)性質(zhì)變差,地層強(qiáng)度降低,相應(yīng)的極易發(fā)生屈服失穩(wěn)。
圖6
圖7為鉆井液高于地層溫差為7 K時,井眼附近0.
3 結(jié)論
1)天然氣水合物地層在鉆井過程中,鉆井液溫度對水合物地層的影響是一個極為復(fù)雜的物理化學(xué)過程,涉及熱傳導(dǎo)、對流及水合物分解,以及地層應(yīng)力狀態(tài)、力學(xué)性質(zhì)的變化,是一個多因素相互耦合的過程,應(yīng)通過多因素耦合的方法來建立描述該過程的數(shù)學(xué)模型。
2)隨著鉆井液高于地層的溫度差越大,井壁附近地層的水合物分解范圍也越大,同時導(dǎo)致地層的強(qiáng)度降低、力學(xué)性質(zhì)變差,相應(yīng)地容易發(fā)生屈服失穩(wěn)。并且疊加上非均勻水平地應(yīng)力的作用,井壁附近地層最小水平地應(yīng)力方向是屈服失穩(wěn)的最危險位置。
3)天然氣水合物地層鉆井過程中,由于井眼液柱壓力一般不得低于地層壓力,溫度是影響地層水合物分解的最主要的因素。基于本數(shù)值模擬的分析,可以看出盡量控制鉆井液的溫度不高于水合物的相平衡溫度,能夠抑制井壁附近地層水合物的分解,進(jìn)而有利于保持井壁的穩(wěn)定。然而,低溫又對鉆井液的流變性等性能提出了較高的要求,所以優(yōu)選出能適用于低溫環(huán)境的鉆井液體系,對提高天然氣水合物地層的井壁穩(wěn)定將有很大幫助。
參考文獻(xiàn)
[l] 竇斌,REINICKE K M.鉆井過程中甲烷水合物的分解特性研究[J].天然氣工業(yè),2007,27(12):83-85.
[2] KOH C A.Towards a fundamental understanding of natural gas hydrates[J].Chemical Society Reviews,2002,31:157-167.
[3] 張旭輝,魯曉兵,李清平,等.水合物沉積層中考慮相變的熱傳導(dǎo)分析[J].中國科學(xué):物理學(xué)力學(xué)天文學(xué),2010,40(8):1028-1034.
[4] 張旭輝,劉艷華,李清平,等.沉積物中導(dǎo)熱體周圍水合物分解范圍研究[J].力學(xué)與實踐,2010,32(2):39-41.
[5] CHAOUCH A,BRIAUD J L.Post melting behavior of gas hydrates in soft ocean sediments[C]//paper 8298-MS-pres-ented at the Offshore Technology Conference,5-8 May,1997,Houston,Texas,USA.Houston:OTC,1997.
[6] RUTQVIST J,MORIDIS G J.Numerical studies on the geomechanical stability of hydrate bearing sediments[C]//paper l8860-MS presented at the Offshore Technology Conference,30 April-3 May,2007,Houston,Texas,USA.Houston:OTC,2007.
[7] KHURSHID l,LEE K J,BAHK J J,et al.Heat transfer and well bore stability analysis in hydrate bearing zone in the east sea,south Korea[C]∥paper 20582 MS presented at the Offshore Technology Conference,3-6 May,2010,Houston,Texas,USA.Houston:OTC,2010.
[8] NAZRIDOUST K,AHMADI G.Computational modeling of methane hydrate dissociation in a sandstone core [J]Chemical Engineering Science,2007,62(22):6155-6177.
[9] KIM H C,BISHNOI P R,HEIDEMAN R A,et al.Kinetics of methane hydrate decomposition[J].Chemical Engineering Science,1987,42(7):1645-1653.
[10] HONG Huifan9.Modeling of gas production form hydrates in porOUS media[D].Calgary:University of Calgary,2003.
[11] XU Wenyue,GERMANOVICH L N.Excess pore pressure resulting from methane hydrate dissociation in marine sediments:a theoretical approach[J].Journal of Geo-physical Research,2006,111:B01104.
[12] NABIL S.Comment on‘Excess pore pressure resulting from methane hydrate dissociation in marine sediments:a theoretical approach’by Wenyue Xu and Leonid N.Germanovich[J].Journal of Geophysical Research,2007,112:78-84.
本文作者:李令東 程遠(yuǎn)方 梅偉 李清平 高立超
作者單位:中國石油大學(xué)(華東)石油工程學(xué)院 中海石油研究中心 中國石油長城鉆探工程公司固井公司
您可以選擇一種方式贊助本站

支付寶轉(zhuǎn)賬贊助

微信轉(zhuǎn)賬贊助