摘要:LNG儲存溫度為-161.5℃,一旦發生泄漏,迅速蒸發后的氣體密度約為空氣密度的1.5倍,低溫的重氣云團將會發生重力沉降;同時,由于大氣湍流將空氣卷吸進入云團內部,低溫重氣云團也會被加熱,向正浮性氣體擴散轉變。為此,研究了LNG大規模持續泄漏產生的氣體擴散問題,建立了LNG泄漏時安全距離的計算方法,并分析對安全距離的影響因素。從DEGADIS重氣擴散基本模型出發,建立了LNG泄漏擴散時的場景條件和計算程序,并考慮了LNG向下風向擴散過程中受熱形成的浮升效應以及風速和大氣不穩定度的影響。所建立的方法比其他方法具有更好的準確性和適用性。通過與LNG泄漏擴散實地實驗(Burro系列實驗)數據進行比較,驗證了該方法的計算結果,平均相對偏差為24.82%。通過研究風速、大氣穩定度、泄漏源大小、圍堰尺寸等因素對LNG氣體擴散的影響,確定了不同條件下LNG擴散的安全距離要求。
關鍵詞:LNG;泄漏;重氣;擴散;安全距離;積分模型;DEGADIS
0 引言
天然氣在常溫下密度比空氣密度小,但LNG儲存溫度為-161.5℃,一旦發生泄漏,迅速蒸發后的氣體密度約為空氣密度的1.5倍[1]。低溫的重氣云團將會發生重力沉降,同時,由于大氣湍流,空氣將被卷吸進入云團內部,低溫的重氣云團也會被加熱,向正浮性氣體(即比空氣密度小的氣體)擴散轉變[2]。
筆者從DEGADIS重氣擴散基本模型出發,建立了LNG泄漏擴散時的場景條件和計算程序,計算模型中考慮了液化天然氣向下風向擴散過程中受熱形成的浮升效應以及風速和大氣不穩定度的影響,給出相應的分析模型和計算方法,并用國際上典型實驗數據加以驗證。重點對液化天然氣大規模持續泄漏產生的氣體擴散問題進行了研究。
1 DEGADIS穩態模型及其驗證
1.1 模型描述
DEGADIS(DEnse GAs DISpersion)模型是由Havens和Spicer在1989年推出的一種用于分析重氣擴散的模型[3],并作為NFPA 59A推薦使用的一種模型,用于評估LNG生產儲運過程中的重氣擴散情況[4]。
連續泄漏模型又稱穩態模型,即下風向云團內部的各種性質參數只是位置的函數。DEGADIS作為積分模型,假設氣體擴散濃度在側風向上采用修正的高斯分布,而豎直方向上采用指數分布,并且對風速分布做了假設,其表達式如下:
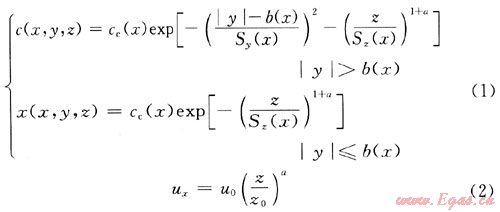
式中下風向不同距離處的擴散系數Sy(x)、Sz(x),以及特征寬度b(x)、密度ρ(x)和溫度T(x)的求解,需要滿足下列守恒及特征擴散參數關系。
總質量守恒:
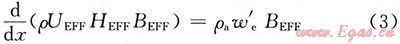
泄漏組分守恒:
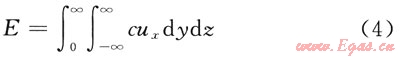
能量守恒:
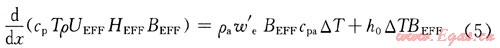
垂直和水平特征擴散參數控制方程[3]:
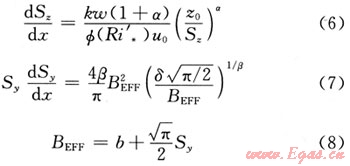
在上述控制方程中的能量方程反映了云團擴散過程受熱后的溫度變化,由此而產生的擴散氣體的密度變化和浮升效應在理查森數及相關的卷吸和擴散特征參數中體現。
上述方程采用數值積分方法聯立求解,其計算程序具有很好的收斂精度。本文建立的計算程序與DEGADIS通用計算程序對比,其計算精度符合很好。利用建立的程序計算得到濃度分布中的擴散參數,進而求出下風向的濃度分布和下風向擴散距離。
1.2 模型驗證
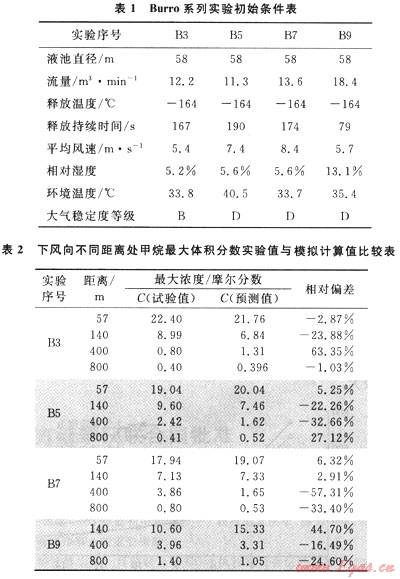
本文研究的數學模型通過Burro系列實驗[1,5]進行驗證,Burro實驗在距離泄漏源下風向57m、140m、400m、800m處分別測得天然氣的最大體積分數值,該實驗共進行了多組,本文對其中的3號、5號、7號和9號實驗進行模擬,將實驗數據與模型計算結果對比,并進行誤差分析,得出模型計算的平均相對偏差為24.28%。實驗的初始條件以及對比結果見表1、2。
2 安全距離的影響因素分析
在LNG場站選址時,需要遠離居民區,以保證人民生命財產安全,因此,場站與居民區之間的距離是重要的考慮因素。LNG在泄漏過程中,自泄漏源開始,氣體濃度逐漸被稀釋,當其體積濃度在5%~15%范圍內(即甲烷的爆炸極限內),存在發生火災或者爆炸的可能性。為了確保間隔距離劃定的可靠性,相關標準(如NFPA59A),規定其下風向體積濃度為2.5%處的距離為安全距離[4]。以Burro系列5號實驗為例(以下簡稱B5),其下風向上體積濃度的等濃度線見圖1,可以看出下風向體積濃度5%和2.5%的最大距離差約為110m。以下用所建的計算模型,對氣體擴散過程和安全距離的影響因素進行分析。

2.1 風速和大氣條件
環境風速是衡量大氣湍流程度的一個必不可少的條件,在LNG重氣擴散過程中,風速對云團下風向的運動速率,云團濃度稀釋,空氣卷吸以及云團加熱等過程有著重要的影響,進而影響安全距離的大小。大氣穩定度是用于衡量大氣湍流程度的一種半定量方法,常用的大氣穩定度分類采用帕斯圭爾(Pasquill)方法[6],將氣象條件分為6種穩定度等級,即A、B、C、D、E、F,可依次定性為極不穩定、不穩定、弱不穩定、中性、弱穩定、穩定。
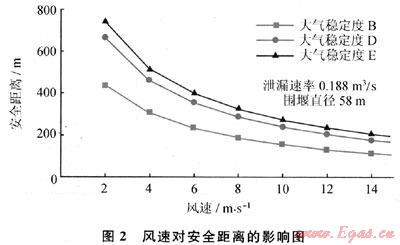
圖2示出B5條件下,大氣穩定度及風速對氣體擴散距離的影響。在同一穩定度等級時,隨著風速增大(風速大于2m/s),安全距離隨之減小。原因在于風速越大,大氣湍流對云團稀釋越迅速,同時重氣效應減弱也越快。隨著大氣條件趨于穩定時,安全距離隨之增加。而在大氣條件不穩定時,大氣卷吸增強會加速云團濃度稀釋,造成擴散距離減小。對于連續泄漏擴散,當風速較小且大氣環境趨于穩定時,安全隱患較大。
2.2 泄漏速率
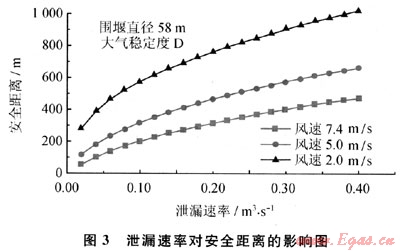
在給定風速條件下,隨著泄漏速率增加,下風向的安全距離也隨之增大(如圖3所示)。泄漏速率大小是影響穩態重氣擴散安全距離的決定因素。
2.3 圍堰尺寸
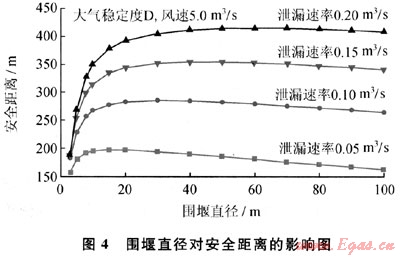
LNG儲罐周圍通常要設計圍堰,以防止儲罐發生泄漏時,液體四處流淌蔓延,若發生火災,還可以防止火焰蔓延到周邊地區[4]。LNG泄漏到圍堰內,會迅速蒸發氣化,形成以圍堰為二次源的蒸氣云團擴散。圖4給出下風向安全距離隨著圍堰直徑和泄漏速率的變化。當圍堰尺寸較小時,以圍堰為二次源云團的范圍也較小,有限的蒸發氣受大氣湍流影響,其濃度較快稀釋,安全距離較小;當圍堰尺寸過于增大時,二次源云團的天然氣濃度較低,其下風向擴散距離不再增加,反而略有減少。
此外,LNG泄漏表面(水面或地面影響蒸發速率)、空氣濕度[7](氣溶膠的影響)、下風向的地形結構等因素也會對重氣擴散過程產生很大影響[8~9],如果地形結構復雜,障礙物較多,風場的風速分布將會發生變化,在障礙物的背風面,會產生低壓回流,使得在小范圍內云團濃度增大。
3 結束語
所建立的LNG泄漏氣體擴散模型計算方法,經過實驗驗證,其平均偏差為24.28%,并較準確地體現了重氣擴散過程中云團內部特性的變化規律。對于穩態LNG氣體擴散,當風速大于2m/s時,隨著風速的增加,安全距離是逐漸減小的;對于較小風速(小于2m/s)時,該穩態模型將不再適用。泄漏速率增大使安全距離幾乎成比例增大,是影響安全距離最重要因素之一。對于給定的LNG泄漏率,圍堰尺寸變化對安全距離的影響會呈現出一個弱峰,之后安全距離會隨圍堰尺寸的增加而略有減小。
本文計算主要反映了LNG大規模持續泄漏的狀況,建立的LNG氣體擴散模型計算方法可供工程上LNG泄漏擴散安全距離的分析和評估采用。
符號說明
BEFF為云團有效半寬度,m;c為云團濃度,kg/m3;cc為地表中心線濃度,kg/m3;Cp為云團定壓比熱,J/(kg·K);Cpa為空氣定壓比熱,J/(kg·K);E為泄漏源強度,kg/s;h0為傳熱系數,J/(m2·K);HEFF為有效云團高度,m;k為卡門系數,0.35;Ri′*為理查森數;u0為環境風速,m/s;UEFF為云團移動速度,m/s;ux為豎直方向風速分布,m/s;w為豎直方向湍流速度,m/s;we′為豎直方向空氣卷吸速度,m/s;x為下風向中心線距離,m;y為側風向距離,m;z為豎直方向高度,m;z0為環境風速測量高度,m;α為豎直方向風速分布指數;β為水平擴散參數系數;δ為水平擴散參數系數(與大氣穩定度相關);ρa為環境空氣密度,kg/m3。
參考文獻
[1] KOOPMAN R P,ERMAK D L.Lessons learned from LNG safety research[J].Journal of Harzardous Materials,2007,140(3):412-428.
[2] 潘旭海,蔣軍成.重氣云團瞬時泄漏擴散的數值模擬研究[J].化學工程,2003,31(1):35-39.
[3] HAVENS J,SPICER T.A dispersion model for elevated dense gas Jet chemical releases[R].[S.l.]:EPA,1988.
[4] Standard for Production,Storage and handling of LNG[S].NFPA 59A,2006:9-15.
[5] MOHAN M,PANWAR T S,SINGH M P.Development of dense gas dispersion model for emergency preparedness[J].Atmosphere Environment,1995,29(16):2075-2087.
[6] 谷清,李云生.大氣環境模式計算方法[M].北京:中國氣象出版社,2002:5-20.
[7] 魏利軍.重氣擴散過程的數值模擬[D].北京:北京化工大學,2000.
[8] 姜傳勝,丁輝,劉國梁,等.重氣連續泄漏擴散的風洞模擬實驗與數值模擬結果對比分析[J].中國安全科學學報,2003,13(2):8-13.
[9] 潘旭海,華敏,蔣軍成.環境條件對LNG泄漏擴散影響的模擬研究[J].天然氣工業,2009,29(1):117-119.
(本文作者:孫標 郭開華 中山大學工學院)
贊 賞 分享
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助




