摘要:偏移速度建模的準(zhǔn)確性直接影響偏移成像的效果。克希霍夫積分法疊前時(shí)間偏移,雖能部分適應(yīng)速度縱橫向的變化,但由于沒(méi)有考慮射線彎曲,所以在速度縱向變化較大時(shí)偏移效果并不理想。而彎曲射線各向異性疊前偏移方法則考慮了成像射線的彎曲及速度各向異性,更有利于消除了地層傾角和反射點(diǎn)彌散的影響,建立的速度模型更準(zhǔn)確、更符合地質(zhì)變化規(guī)律。采用沿層速度分析技術(shù)獲得目的層面上準(zhǔn)確的速度信息,通過(guò)CRP反偏移速度分析技術(shù)逐步優(yōu)化速度模型,借助彎曲射線疊前時(shí)間偏移方法取得顯著的成像效果。同時(shí)指出了在速度縱橫向變化劇烈、地下構(gòu)造復(fù)雜時(shí),深度偏移才能恢復(fù)地下真實(shí)構(gòu)造形態(tài)。采用相干反演法與均方根速度轉(zhuǎn)換法聯(lián)合建立層速度模型,利用層析成像技術(shù)優(yōu)化地質(zhì)模型,通過(guò)深度偏移方法研究和偏移效果的對(duì)比,總結(jié)了建立精確偏移速度場(chǎng)的方法和步驟,使速度建
關(guān)鍵詞:地震勘探;偏移成像;射線路徑;速度;分析;波動(dòng)方程;數(shù)學(xué)模型;效果
1 時(shí)間域速度分析與偏移成像
疊后時(shí)間偏移無(wú)法考慮射線傳播的折射效應(yīng),致使聚焦不良[1]。疊前時(shí)間偏移成為時(shí)間域成像的最佳選擇。特別是彎曲射線各向異性疊前時(shí)間偏移比疊后時(shí)間偏移取得更理想的成像效果,采用沿層連續(xù)速度分析技術(shù)獲得層面上準(zhǔn)確的疊加速度(比常規(guī)的隔線分析速度信息量大、精度高),通過(guò)傾角校正及CRP反偏移速度分析技術(shù)逐步優(yōu)化速度,得到符合地質(zhì)規(guī)律的準(zhǔn)確的均方根速度場(chǎng),為建立層速度場(chǎng)奠定基礎(chǔ)。
1.1 沿層連續(xù)速度分析
沿層連續(xù)速度分析是沿時(shí)間域的層位T0時(shí)間計(jì)算逐個(gè)CMP的疊加速度。沿層速度譜使目的層界面上的速度信息量增加,極大地提高了速度的橫向分辨率,同時(shí)由于以層位進(jìn)行速度分析,速度平面圖能大體反映出構(gòu)造形態(tài)變化,特別是地層的傾角變化情況。
1.2 基于CRP道集的均方根速度分析
將沿層反演出的疊加速度進(jìn)行傾角校正轉(zhuǎn)換成均方根速度,利用CRP道集反動(dòng)校的方法進(jìn)行速度優(yōu)化(圖1)。從對(duì)比圖中可以看出,由于疊前時(shí)間偏移消除了地層傾角和反射點(diǎn)彌散的影響,得到的CRP反映同一反射點(diǎn)的信息,此時(shí)時(shí)距曲線更接近雙曲線理論假設(shè),分析的均方根速度更準(zhǔn)確、更符合地質(zhì)變化規(guī)律。
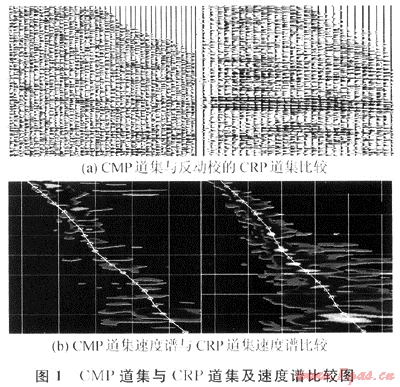
1.3 疊前時(shí)間偏移
克希霍夫積分法偏移最主要的特性之一就是它能夠基于地震記錄,選擇激發(fā)點(diǎn)和相應(yīng)的地震波射線束進(jìn)行目標(biāo)偏移成像[2]。
假設(shè)介質(zhì)是均勻且為完全彈性,縱波波動(dòng)方程為:
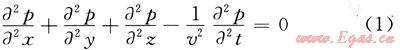
式中:v為波的傳播速度,m/s;p為波場(chǎng)函數(shù)。
假設(shè)閉合曲面S0由A0和A兩部分組成,其中A0是地面觀測(cè)平面,A為部分球面,球面半徑趨于無(wú)窮大。故式(1)可表示為:
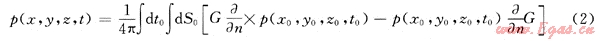
式中:p(x,y,z,t)為閉合曲面S0上某個(gè)觀測(cè)點(diǎn)R(x,y,z)處的波場(chǎng)函數(shù)值;p(x0,y0,z0,t0)為閉合曲面S0上某個(gè)觀測(cè)點(diǎn)R0(z0,y0,z0)處的波場(chǎng)函數(shù)值;n為閉合曲面的外法線方向;G為格林函數(shù)。
根據(jù)邊界條件,由式(2)推導(dǎo)出克希霍夫積分式:
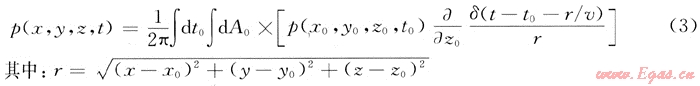
故可得到:
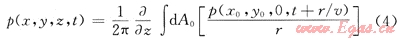
根據(jù)成像理論,t=0時(shí)實(shí)現(xiàn)三維空間偏移歸位:
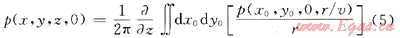
1.4 射線彎曲理論
對(duì)于雙均方根公式,通過(guò)高階項(xiàng)逼近得到提高。即
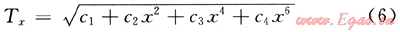
修改系數(shù)c4可簡(jiǎn)化為:
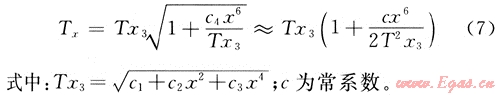
對(duì)于3D Kirchhoff疊前時(shí)間偏移而言,總旅行時(shí)可表示為:
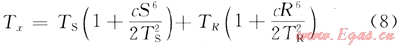
式中:S、R為炮檢點(diǎn)到成像點(diǎn)的距離[3]。
克希霍夫積分法疊前時(shí)間偏移,考慮了復(fù)雜陡傾界面的地層傾角及反射點(diǎn)彌散問(wèn)題,能部分適應(yīng)速度在縱橫向的變化[4]。由于沒(méi)有考慮射線彎曲,所以在速度縱向變化較時(shí)偏移效果不理想彎曲射線各向異性疊前時(shí)間偏移,由于它考慮了成像射線的彎曲及速度各向異性,更符合地下實(shí)際,成像效果明顯優(yōu)于直射線疊前時(shí)間偏移,在斷層成像、斷塊劃分能力以及目的層內(nèi)幕反射特征上有很大的改善(圖2)。

2 深度域速度分析與偏移成像
2.1 層速度模型與深度模型的建立
采用均方根速度轉(zhuǎn)換方法估算層速度與相干反演相結(jié)合的方法進(jìn)行層速度模型的建立。通過(guò)疊前時(shí)間偏移迭代后,均方根速度模型比較準(zhǔn)確,在一定程度上符合地質(zhì)變化規(guī)律。對(duì)于水平層狀或單傾的介質(zhì),均方根速度模型轉(zhuǎn)換的方法能得到較好的初始模型,并通過(guò)層析成像模型優(yōu)化能得到精確的速度模型。對(duì)于地層傾角變化較大、速度不均一的復(fù)雜斷塊,簡(jiǎn)單的速度轉(zhuǎn)換方法不能合理地描述速度結(jié)構(gòu)。采用相干反演法與均方根速度轉(zhuǎn)換法聯(lián)合建立層速度模型,相互驗(yàn)證速度的合理性精度更高。通過(guò)分析沿層剩余速度,利用三維層析成像技術(shù)修改層速度模型優(yōu)化地質(zhì)模型,建立最優(yōu)速度-深度模型剛(圖3)。

2.2 三維疊前深度偏移方法對(duì)比
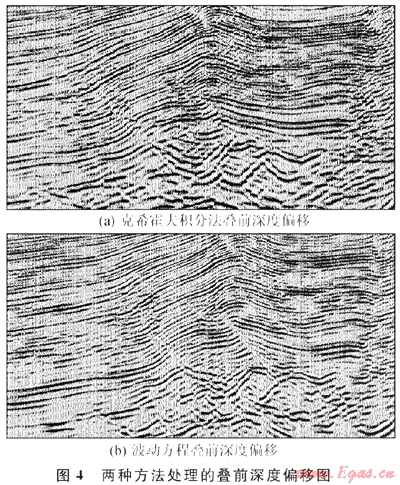
三維疊前深度偏移方法主要采用克希霍夫積分法,優(yōu)點(diǎn)是計(jì)算效率高,對(duì)野外觀測(cè)無(wú)任何限制適應(yīng)能力強(qiáng),且能較好的適應(yīng)大傾角偏移,具有抗假頻能力;缺點(diǎn)是射線多路徑問(wèn)題、焦散、振幅保真處理問(wèn)題和分辨率低等。研究人員通過(guò)兩種途徑來(lái)解決不足:①對(duì)現(xiàn)有的克希霍夫法在旅行時(shí)計(jì)算和偏移方法方面進(jìn)行改進(jìn),如從首波旅行時(shí)計(jì)算向基于波前重建的旅行時(shí)計(jì)算,其中考慮了多個(gè)射線,并且是利用體波旅行時(shí)、相對(duì)保幅處理和基于模型的孔經(jīng)定義等,改進(jìn)后的成像結(jié)果其構(gòu)造細(xì)節(jié)更加清楚可靠;②發(fā)展新的偏移方法,借助于高性能的PC-CLUSTER微機(jī)集群,采用波動(dòng)方程偏移方法,其成像結(jié)果更好。圖4可看出波動(dòng)方程疊前深度偏移在深層斷點(diǎn)歸位準(zhǔn)確、振幅頻率保持較好,成像精度更高[6]。
3 結(jié)束語(yǔ)
綜上所述,各向異性彎曲射線疊前時(shí)間偏移比直射線疊前時(shí)間偏移在成像能力上有更大優(yōu)勢(shì)。但在速度縱橫向變化劇烈時(shí),要恢復(fù)地下構(gòu)造形態(tài)及復(fù)雜斷塊成像時(shí),必須進(jìn)行深度偏移。盡管疊前深度偏移方法是提高成像精度的必要手段,但真正影響成像精度的是速度模型。因此,層速度反演及精細(xì)速度建模成為疊前深度偏移處理的關(guān)鍵環(huán)節(jié)。從克希霍夫積分法與波動(dòng)方程疊前深度偏移的研究對(duì)比結(jié)果中可以看出,波動(dòng)方程疊前深度偏移斷點(diǎn)歸位準(zhǔn)確、頻率振幅特征保持較好,在復(fù)雜構(gòu)造成像及巖性勘探中確實(shí)有它的優(yōu)勢(shì),是解決復(fù)雜構(gòu)造地震資料處理的新途徑。但是克希霍夫積分算法有很強(qiáng)的適應(yīng)性和高效的運(yùn)算能力及目前不斷改進(jìn)的算法提高了偏移精度。因此,可以結(jié)合兩種算法的優(yōu)勢(shì),取得更好的偏移效果。
參考文獻(xiàn)
[1] 熊翥.復(fù)雜地區(qū)地震數(shù)據(jù)處理思路[M].北京:石油工業(yè)出版社,2002.
[2] 王棣,王華忠,馬在田,等.疊前時(shí)間偏移方法綜述[J].勘探地球物理進(jìn)展,2004,27(5):312-319.
[3] SUN CH,MARHINEZ R D. Amplitude preserving V(z)pre stack Kirchhoff time migration for VTI media[J].First Break,2001,19:618-624.
[4] 羅銀河,劉江平,董橋梁,等.Kirchhoff彎曲射線疊前時(shí)間偏移及應(yīng)用[J].天然氣工業(yè),2005,25(8):35-37.
[5] 張建偉,強(qiáng)芳青,賀振華,等.三維疊前深度偏移在復(fù)雜斷裂區(qū)的應(yīng)用[J].天然氣工業(yè),2004,24(3):52-54.
[6] 張敏,李振春.偏移速度分析與建模方法綜述[J],勘探地球物理進(jìn)展,2007。30(6).422-426.
(本文作者:王小衛(wèi)1,2 劉文卿2 徐興榮2 張小美2 蔣波2 1.中國(guó)地質(zhì)大學(xué);2.中國(guó)石油勘探開(kāi)發(fā)研究院西北分院)
贊 賞 分享
您可以選擇一種方式贊助本站

支付寶轉(zhuǎn)賬贊助

微信轉(zhuǎn)賬贊助
- 注解:本資料由會(huì)員及群友提供僅供閱讀交流學(xué)習(xí),不得用于商業(yè)用途!
網(wǎng)站VIP會(huì)員無(wú)限制下載網(wǎng)站資料!贊助網(wǎng)站獲得,點(diǎn)擊贊助!!
