摘 要:為了提高天然氣短期負荷的預測精度,提出了基于小波變換和LSSVM DE(Least Squares Support Vector Machine Differential Evolution)的天然氣日負荷組合預測模型,首先,采用Mallat快速算法對天然氣日負荷實際采集數據樣本時間序列進行小波分解;其次,對分解出來的高頻分量和低頻分量分別建立LSSVM預測模型,各分量的模型參數分別采用DE進行優化,以期得到更準確的預測結果;最后,分別對各分量的預測結果進行小波重構。以某市實際采集的樣本數據為例,并將重構結果與單獨應用LSSVM預測模型及ANN(Artificial Neural Networks)預測模型進行對比分析。結果表明:小波變換和LSSVM-DE預測模型的預測精度分別比單獨應用LS-SVM和ANN預測模型高出1.662%、1.14%、3.96%、2.99%、15.53%和1.942%、1.01%、3.07%、1.86%、12.26%。該結論預示著將小波變換和LSSVM-DE理論相結合對天然氣日負荷時間序列進行預測是一種行之有效的方法。
關鍵詞:天然氣日負荷 小波分解 LSSVM-DE ANN 小波重構 預測 精度
A forecasting model of natural gas daily load based on wavelet transform alld LSSVM-DE
Abstract:In order to improve the accuracy of predicting the short term natural gas load,a forecasting model of natural gas dailv load was built based on wavelet transform and LSSVM DE(Least Squares Support Vector Machine-Differential Evolution).First,the Mallat algorithm was applied to conduct the wavelet decomposition of the time series in a sample of the actual gas dailv load data.Then,the LSSVM forecasting model was established for the decomposed high and low frequency components respectively,the parameters of which were optimized by using the DE to achieve more accurate forecasting results.Finally,we re-constructed the wave1et of each component+s forecasting result.In a case study from a certain city,a comparative analysis was made of the forecasting resuits between the combined use of wavelet transform and LSSVM DE and the independent use of LSSVM or ANN(artificial neural networks).The forecasting model based on wavelet transform and LSSVM-DE was validated with a high prediction accuracy and the resulted relative mean square error,normalization mean square error,normalization absolute square error,normalization root mean square error,maximum absolute error resulted from the combined use of wavelet transform and LSSVM-DE were lower than those from the independent u,se of LSSVM or ANN by 1.662%,1.14%,3.96%,2.99%,15.53%,1.942%,1.01%,3.07%,1.86%and l2.26%respectively.In conclusion,this study provides a practical and feasible method for predicting the time series of natural gas daily load.
Keywords:gas daily load,wavelet decomposition,LSSVM-DE,ANN,wavelet reconstruetion,forecast
隨著我國天然氣工業的大力發展,燃氣企業的市場化運作,作為燃氣企業重要組成部分的負荷預測受到越來越多的重視。近年來,同家積極提倡節能減排,因而對天然氣短期負荷的預測精度提出更高的要求。天然氣短期負荷是一個復雜的非線性系統[1],系統本身具有偽周期性、隨機性和趨勢性等特點,此外天然氣短期負荷也與溫度等多種氣象自然因素息息相關,同時還受重大事件及國家法定節假目的影響。因此,建立精確的負荷預測模型具有重要的意義。
現有的天然氣短期負荷預測方法主要包括兩種:一種是物理方法[2],其利用天氣預報的結果如溫度、濕度、風速、云量等物理信息建立刻畫天然氣短期負荷的模型進行預測;另一種是統計方法,即根據過往的歷史樣本數據建立系統輸入與輸出的非線性映射關系來進行預測,如小波分析綜合模型[3]、GM(1,1)灰色理論模型[4]、BP神經網絡模型[5]、時間序列模型[6]等。物理方法不需要大量實測的歷史樣本數據,但是預測誤差較大,而統計方法共同的特點是預先建立時間序列的主觀預測模型,然后根據建立的主觀預測模型進行計算及預測。對于絕大多數由實際測量數據所組成的系統(尤其是城市天然氣日負荷)來說,其外部影響條件,包括天氣、節假日、經濟及異常情況等,都隨著時間的變化而變化,不會保持恒定,這樣的系統往往表現出波動性、非平穩性的特征,劉涵[7-8]等利用最小二乘支持向量機進行天然氣日負荷預測時,考慮了天氣、節假日、經濟及異常情況的影響,但其未對日負荷預測的波動性規律進行分析,所以是否可以考慮將小波變換和LSSVM這兩種方法相結合并應用到日負荷預測中,以提高預測精度,筆者試圖從這一思路著手來提高天然氣日負荷預測的預測精度。
筆者以某市2013年4月1日至2013年8月31日實際采集的天然氣日負荷時間序列為例進行研究。首先,對該時間序列進行小波分解,母小波采用Db3(Daubechies3)分解為3層,運用MATLAB軟件,分解出第3層低頻信號序列、第1層高頻序列、第2層高頻序列、第3層高頻序列,以識別日負荷時間序列的波動特性;其次,分別采用LSSVM-DE、LSSVM、ANN預測模型對分解出的第3層低頻信號序列、第1層高頻序列、第2層高頻序列、第3層高頻序列進行預測;最后,對預測結果進行小波重構,該過程為小波分解的逆過程。為了評價各預測模型的預測精度,采用國際上普遍采用的5種定量評價方法進行評價。結果表明:小波變換和LSSVM-DE組合預測模型的預測精度明顯高于單獨應用LSSVM、ANN預測模型,為實際工程的在線應用提供了理論基礎。
1 小波變換基本理論
1.1 小波分解
時間序列進行小波分解與重構的常用算法統稱為Mallat算法,該算法與快速Fourier變換相類似,具有快速、簡潔的特點,因此被廣泛應用[9-10]。將天然氣日負荷時間序列看成復雜信號,采用Mallat快速算法對其進行分解,分解出不同頻帶的信號,分析不同頻帶的信號,可得到時間序列信號的一些特征,考慮到分解層數多可能引起累積誤差,造成對預測精度的影響,筆者采用3層分解,母小波采用Db3小波,分解算法如圖1所示。
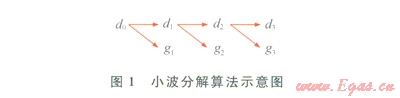
圖1中d0,為原始信號序列,d3為第3層低頻信號序列,g1、g2、g3分別為第1層高頻序列、第2層高頻序列、第3層高頻序列,圖1依據的公式為:
dj=ldj+1 (1)
gj=hgj+1 (2)
式中l為低通濾波器系數;h為高通濾波器系數。
1.2 小波重構
小波藿構算法與小波分解算法的過程相反[11],重構算法如圖2所示。
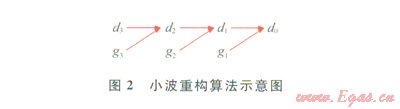
圖2依據的公式為:
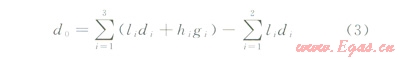
2 LSSVM(最小二乘支持向量機)基本理論
支持向量機是由Vapnik在統計學習理論的基礎上建立起來的一種很有潛力和新的機器學習方法[12-13],該方法的基本思想為:給定訓練樣本集(xi,yi),i=1,…,m,x,∈R,選擇一非線性映射j(x)把樣本的輸入向量空間映射到高維空間F,然后在此空間上構造最優線性決策函數。
f(x)=wj(x)+b (4)
式中w為權值向量;b為一個偏量。
根據結構風險最小化原理,引入間隔的概念,并考慮擬合誤差(ξi)和函數的復雜度,得出優化問題為:
min1/2wTw+1/2g∑ξi2 (5)
約束條件為:
yi[wTj(xi)+b]=1-ξi,i=1,…,m (6)
式中g為正則化參數;T為矩陣的轉置。
針對天然氣日負荷預測問題,筆者認為該問題屬于回歸問題,因此選擇LSSVM進行預測。
令C=g/2,則最小二乘支持向量機的優化問題為:
min1/2wTw+C∑ξi2 (7)
約束條件為:
yk=wTj(xi)+b+ξi,i=1,…,m (8)
式中C為懲罰因子。
對應于優化問題式(7)、(8)的Lagrange函數為:
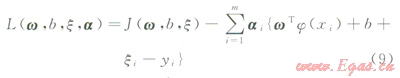
式中ai為Lagrange乘子。
根據KKT(Karush-Kuhn-Tucker)條件[13]可得如下方程組:
式中Wij=j(xi)Tj(xj)=K(xi,xj),Y=(y1,…,ym)T,1=(1,…,1)T,a=(a1,…,am)T。
將式(10)變形為:
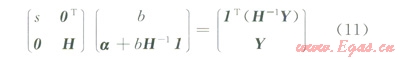
式中H=Wij+g-1I,s=1T(H-11)。
求解式(11)可參照本文參考文獻[12],可得變量a和b,寫成統一的形式為:
Hx=d (12)
由于H是對稱正定的,上述方程用超松弛迭代法來求解,解出a和b后,將a和b帶入下面的方程:
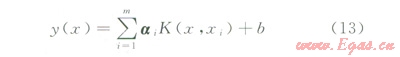
式中K(x,z:)為核函數,本文選用高斯徑向基核函數,其形式為:
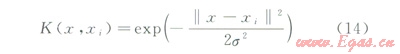
式中s為核寬度。
3 基于小波變換和LSSVM-DE的天然氣日負荷預測模型
3.1 小波分解
實驗軟件采用Matlab小波分解工具箱,母小波采用Db3小波,分解層數為3層,根據式(1)、(2)進行小波分解。
3.2 LSSVM預測
實驗軟件采用LSSVMLAB軟件,根據LSSVM優化回歸理論可知:高斯徑向基核函數核寬度(s)以及懲罰因子(C)對預測精度影響較大。s和C的求解方法一般為將巧和C分別采用單獨的優化方法進行優化,筆者采用組合優化方法進行參數組合優化,具體為差分進化算法[14](DE),LSSVM預測模型的預測參數見表1。
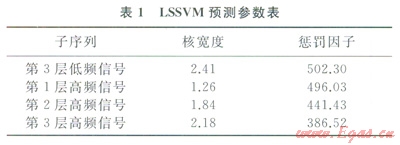
3.3 小波重構
小波重構為小波分解的逆過程,基本條件同小波分解,根據式(3)進行小波重構。
4 實例研究
為了驗證筆者提出的基于小波變換和LSSVM-DE的天然氣日負荷預測模型的預測精度,選取某市2013年4月1日—2013年8月31日的l53個數據作為樣本點,選取2013年9月1日—2013年9月30日的30個數據作為驗證,并與單獨應用LSSVM和ANN預測模型進行對比分析,日負荷隨時間變化如圖3所示,從圖3可以看出除個別樣本點值突變較大外,其余各點日負荷用氣量值在27500~40000m3波動,并表現出非平穩性。
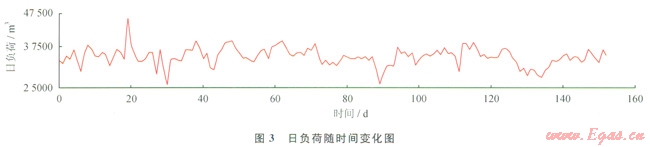
4.1 小波分解
小波分解結果如圖4所示。
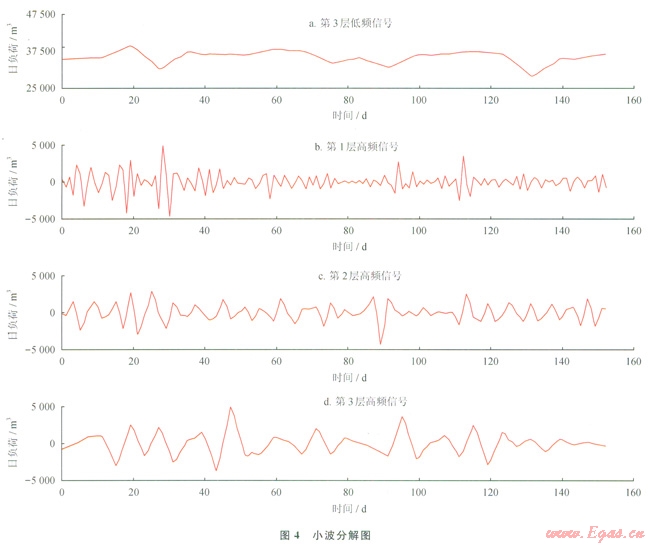
4.2 LSSVM各層預測
4.2.1影響因素分析
影響天然氣日負荷變化的主要影響因素有:日期類型因素、天氣因素、經濟因素、異常情況。下面就其中主要的節假日因素和天氣因素進行分析。
4.2.1.1節假日因素
城市天然氣用戶在平常日、星期六和星期天、重大節日的天然氣用氣量具有明顯的差異,在預測中必須要將這種差異考慮進去,否則就會出現星期六和星期天、重大節日欠預測、平常日過預測的現象。
4.2.1.2天氣因素
據本文參考文獻[2]可知,在各種氣象因素(包括溫度、適度、天氣狀況、風速等)中,對城市天然氣用戶用氣量影響較大的是溫度,尤其是日平均溫度。根據其分析可知:4個季節中,冬季和夏季對其影響較大,并提出了冬季和夏季的城市天然氣日負荷與日平均溫度的相關系數,分別為-0.6288(冬季)和-0.2599(夏季),說明城市天然氣日用氣量與日平均溫度呈負相關,換句話說,溫度升高,日負荷量減少;溫度降低,日負荷量增加,而且冬季受日平均溫度影響較大。
應用LSSVM預測時,考慮節假日因素、天氣因素對預測結果影響較大,因此輸入向量為三維向量,分別為節假日權重系數、日平均溫度、天然氣日負荷,其中節假日權重系數參考本文參考文獻[2],具體見表2,日平均溫度參考2012年同日的實際數據。

4.2.2各層預測結果
各層信號預測結果見圖5。
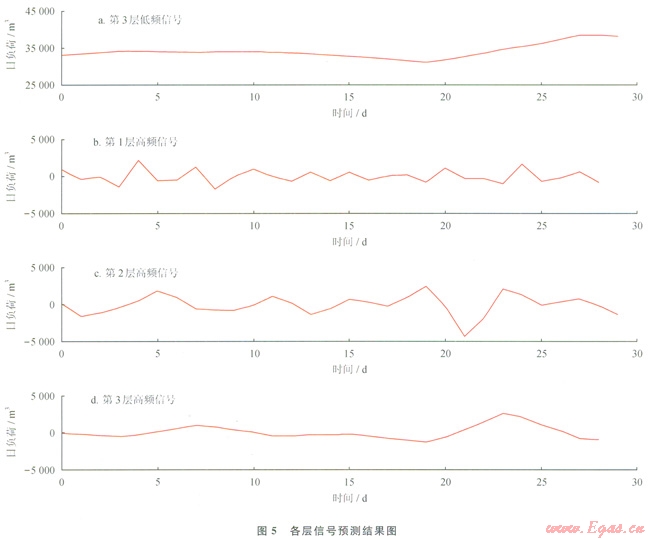
4.3 小波重構
小波重構結果如圖6所示。
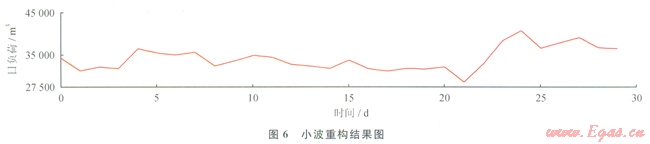
4.4 對比分析
天然氣日負荷預測的常用模型有LSSVM預測模型、ANN預測模型,將筆者所建立的小波變換和LSSVM-DE組合預測模型與上述兩種常用的預測模型進行對比,采用的定量評價方法為國際上普遍采用的5種誤差評價方法,分別為相對均方誤差、歸一化均方誤差、歸一化絕對平方誤差、歸一化均方根誤差、最大絕對誤差,具體公式叮參照本文參考文獻[15]。定量評價結果見表3,定性評價結果見圖7。
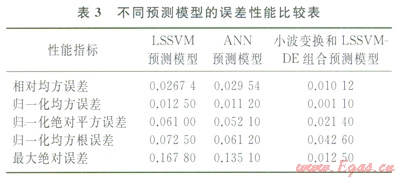
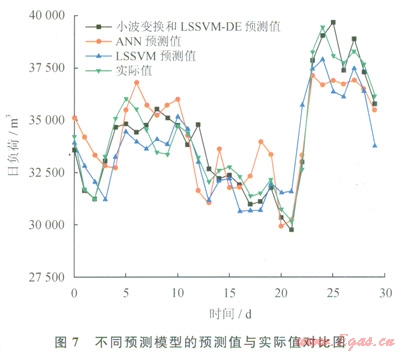
分析圖7和表3可知:小波變換和LSSVM-DE組合預測模型較單獨應用LSSVM、ANN預測模型所得的預測值與實際值更為接近,主要是因為經小波分解處理后,濾掉了原始時間序列的非顯著信息,消除了非顯著信息對預測結果的影響。因此,小波變換和LSSVM-DE組合模型預測值與實際值最接近。從定量方面來看,組合預測模型的相對均方誤差、歸一化均方誤差、歸一化據對平方誤差、歸一化均方根誤差、最大絕對誤差分別比單獨應用LSSVM、ANN預測模型分別低1.662%、1.14%、3.96%、2.99%、15.53%和1.942%、1.01%、3.07%、1.86%、12.26%,各個誤差指標均為正數,表明所建組合模型預測精度較高,能夠準確預測天然氣日負荷,同時能夠緊跟其變化趨勢,尤其是1日4日之間、13日—30日之間,5日—12日之間雖然與實際值存在誤差,但是相比其他兩種預測方法,預測誤差較小。ANN預測模型雖然也能較好地跟隨實際運行數據的變化趨勢,但其預測效果仍然遠不及組合預測模型和單獨應用LSSVM預測模型的預測效果。
5 結論
提出了一種基于小波變換和LSSVM-DE的組合預測模型,相比單獨應用LSSVM、ANN預測模型,組合預測模型具有較高的預測精度,為天然氣負荷預測提供了一種新的思路。
1)采用快速Mallat算法對實際采集的天然氣日負荷時間序列進行小波分解,分解出第3層低頻序列、第1層高頻序列、第2層高頻序列、第3層高頻序列。
2)分別采用LSSVM DE對分解出的各序列進行預測,單獨應用LSSVM、ANN對原天然氣日負荷時間序列進行預測。
3)對LSSVM-DE預測模型的各序列預測結構進行小波重構,將重構結果與單獨應用LSSVM、ANN預測模型的預測結果進行對比分析,結果表明所建組合模型能夠取得很好的預測效果,具有較高的預測精度,為工程應用提供了有益的參考。
參考文獻
[1]焦文玲,廉樂明,崔建華,等.城市燃氣短期周期負荷預測的時序模型[J].天然氣工業,2002,22(1):92-94.
JIAO Wenling,LIAN Leming,CUI Jianhua,et al.Time series model of prediction short period city gas load[J].Natural Gas Industry,2002,22(1):92-94.
[2]何春營,段言志,鄔宗婧,等.基于氣溫的城市燃氣短期日負荷預測模型—一以四川省成都地區為例[J].天然氣工業,2013,33(4):131-134.
HE Chunlei,DUAN Yanzhi,WU Zongjing,et al.A shortterm forecasting model of city gas daily load based on air temperatureFJ].Natural Gas Industry,2013,33(4):131-134.
[3]李持佳,焦文玲,趙林波.燃氣短期負荷預測的小波分析綜合模型[J].天然氣工業,2007,27(8):103-105.
LI Chijia,JIAO Wenling,ZHAO Linbo.A synthesis wavelet analysis method for short term gas load predietion[J].Natural Gas Industry,2007,27(8):103-105.
[4]焦文玲,展長虹,廉樂明,等.城市燃氣短期負荷預測的研究[J].煤氣與熱力,2001,21(6):483-486.
JIAO Wenling,ZHAN Changhong,LIAN Leming,et al.Study of forecasting for short term load of city gas[J].Gas&Heat,2001,21(6):483-486.
[5]楊昭,劉燕,苗志彬,等.人工神經網絡在天然氣負荷預測中的應用[J].煤氣與熱力,2003,23(6):331-332.
YANG Zhao,LIU Yan,MIAO Zhibin,et al.Application of neural network in natural gas load forecasting[J].Gas&Heat,2003,23(6):331-332.
[6]焦文玲,趙林波,秦裕琨.城市燃氣負荷非平穩時序預測模型的研究[J].煤氣與熱力,2003,23(8):451-453.
JIAO Wenling,ZHAO Linbo,QIN Yukun.Study on load forecast of city gas with unstable time series model[J].Gas&Heat,2003,23(8):451-453.
[7]劉涵,劉丁,鄭崗,等.基于最小二乘支持向量機的天然氣負荷預測[J].化工學報,2004,55(5):828-832.
LIU Han,LIU Ding,ZHENG Gang,et al.Natural gas load forecasting based on least squares support vector machine[J].Natural Gas Industry,2004,55(5):828-832.
[8]苗艷姝.城市燃氣負荷預測的研究[D].哈爾濱:哈爾濱工業大學,2006.
MIAO Yanshu.Research on the city gas load forecasting[D]Harbin:Harbin Institute of Technology,2006.
[9]宋彤,李菡.基于小波回聲狀態網絡的混沌時間序列預測[J].物理學報,2012,61(8):90-96.
SONG Tong,LI Han.Chaotic time series prediction based on wavelet echo state network[J].Acta Physica Sinica,2012,61(8):90-96.
[10]朱佳,王振會,金天力,等.基于小波分解和最小二乘支持向量機的大氣臭氧含量時間序列預測[J].氣候與環境研究,2010,15(3):295-302.
ZHU Jia,WANG Zhenhui,JIN Tianli,et al.Combination of wavelet decomposition and least square support vector machine to forecast atmospheric ozone content time series[J].Climatic and Environmental Research,2010,15(3):295-302.
[11]劉明才.小波分析及其應用[M].北京:清華大學出版社,2005:32-34.
LIU Mingcai.Wavelet analysis and its applications[M].Beijing:fsinghua University Press,2005:32-34.
[12]楊曉偉,郝志峰.支持向量機的算法設計與分析[M].北京:科學出版社,2013:63-69.
YANG Xiaowei,HAO Zhifeng.Design and analysis of the support vector machine algorithm[M].Beijing:Science Press,2013:63-69.
[13]周淙,孫威,任海軍,等.基于最小二乘支持向量機和負荷密度指標法的配電網空間負荷預測[J].電網技術,20ll,35(1):66-71.
ZHOU Quan,SUN Wei,REN Haijun,et al.Spatial load forecasting of distribution network based on least squares support vector machine and load density index system[J].Power System Technology,2011,35(1):66-71.
[14]張文專,龍義,焦建軍.基于差分進化算法的混沌時間序列預測模型參數組合優化[J].物理學報,2012,6l(22):120-126.
ZHANG Wenzhuan,LONG Wen,JIAO Jianjun.Parameter determination based on composite evolutionary algorithm for reconstructing phase-space in chaos time series[J].Acta Physica Sinica,2012,6l(22):120-126.
[15]張學清,梁軍.風電功率時間序列混沌特性分析及預測模型研究[J].物理學報,2012,6l(19):70-81.
ZHANG Xueqing,LIANG Jun.Chaotic characteristics analysis and prediction model study on wind power time series[J].Acta Physica Sinica,2012,61(19):70-81.
本文作者:喬偉彪 陳保東 吳世娟 李朝陽 毛建設 馬劍林
作者單位:中國石油大學(華東)儲運與建筑工程學院
遼寧石油化工大學石油天然氣工程學院
華潤(南京)市政設汁有限公司
西南石油大學石油與天然氣工程學院
中國石油集團工程設計有限責任公司西南分公司
中石油煤層氣有限責任公司
中國石油西南管道公司
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助
