摘　要：介紹求解直埋供熱管道空間折角的計算方法，對實際工程中為躲避障礙物采取的多管段連續折角的設計方法進行了探討。

關鍵詞：直埋供熱管道；  空間折角；  連續折角

Calculation of Space Angle and Design of Joint Angle in Heating Pipe

Abstract：The method to calculate the space angle in directly buried heating pipe is introduced．The design method of joint angle in order to avoid the obstacles i n practical engineering is discussed．

Keywords：directly buried heating pipe；space angle；joint angle

直埋供熱管道在敷設過程中經常遇到障礙物，不可避免地需要改變方向。條件允許時，我們可以定制預制彎管，但更多的時候受到現場條件和施工工期限制，無法定制預制彎管，只能現場對管道打坡口，拼接角度焊接，這樣管道就出現了折角。由于直埋供熱管道存在熱伸長和熱應力，必須對折角這樣的管系薄弱節點進行應力驗算，只有通過應力驗算才能保證折角的安全。因此，折角計算與設計方案就顯得非常重要，本文對供熱管道空間折角計算與多管段連續折角設計進行探討。

1　空間折角的計算

判定折角是否安全的第一步是先測量或計算出折角的角度。實際工程中除了平面角外，也經常出現空間折角，必須求出空間折角的值，進而進行應力驗算。

若在CAD軟件中測量兩條直線的夾角，必須自定義坐標系，把兩條直線放在一個平面坐標系內，再測量夾角，這樣才能測量出真實的角度，否則測量的角度為在標準水平或垂直面內投影的夾角。

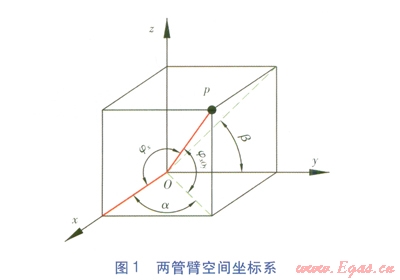
利用CAD軟件求解空間折角的優勢是直觀、準確，但是需要較多步驟和計算機操作技巧。更重要的是，在許多情況下(如在施工現場等)，無法提供給我們適合的計算機操作環境，只能通過手工計算求解。設定兩根管臂中的一根管臂所在直線為x軸，這樣我們只需計算出另一根管臂與x軸的夾角。兩管臂空間坐標系見圖1，一根管臂為x軸，另一個管臂(非x軸管臂)在xOy面(水平面)上的投影與x軸夾角為a，與xOy面夾角為jxOy，兩管臂空間折角為jx。

設管臂上點P的坐標為(x，y，z)，則有：

公式1-3

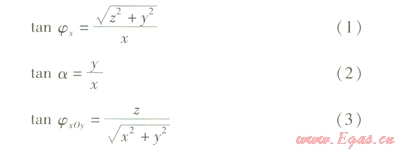
式中jx——管段兩臂空間折角，(°)

z、y、x——z、y、x軸坐標，m

a——非x軸管臂在xOy面上的投影與x軸夾角，(°)

jxOy——非x軸管臂與xOy面夾角，(°)

由式(2)、(3)可得：

z=xsec　atan　jxOy    (4)

由式(1)、(2)、(4)可得：

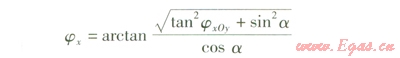
在實際設計中，還有這樣的情況：其他條件不變，非戈軸管臂在xOy面上的投影與x軸夾角a未知，已知非x軸管臂在yOz面的投影與t軸夾角為b，見圖1。這種條件下，jx的計算式為：

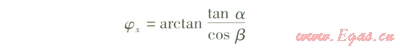
式中b——非戈軸管臂在yOx面的投影與y軸夾角，(°)

2　多管段連續折角的設計計算

①原理

在直埋供熱管道的實際設計與施工中經常遇到設計路由上有障礙物且無法移走的情況，因此管道必須局部改變方向(包括水平面、豎直面上的方向改變)，避讓障礙物，通過后還需調整回原路由。由于現場這樣的情況非常多，因此若每遇到這種情況都采用預制彎管，一方面需要增加大量的預制彎管數量，使工程造價提高；另一方面，定制預制彎管的時間很長，延長了工期，這往往是不可行的。因此，實際工程中常采用多管段連續折角的方法處理。管躲避障礙物時多管段連續折角的布置方式見圖2。

②計算方法

設管段之間的最大允許折角(根據文獻[1]表8-1確定)為g，實際折角為q，且q≤g，每根管段的長度為L，沿管道初始方向為x軸，垂直于管道初始方向為y軸。多管段連續折角圖解見圖3。

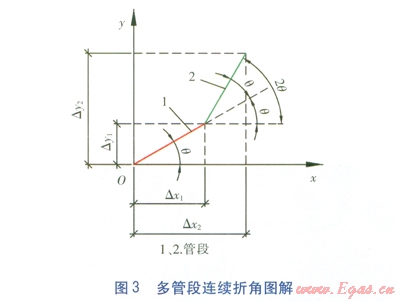
管段1折角后管段在石軸上的行進距離Dx1及在y軸上的偏移量Dy1的計算式分別為：

Dx1=Lcosq

Dy1=Lsinq

式中Dx1——管段1折角后管段在x軸上的行進距離，m

Dy1——管段1折角后管段在y軸上的偏移量，m

L——每根管段的長度，m

q——實際折角，(°)

管段2折角后管段在x軸上的行進距離Dx2及在y軸上的偏移量Dy2的計算式分別為：

Dx2=Lcosq+Lcos 2q

Dy2=Lsinq+Lsin 2q

式中Dx2——管段2折角后管段在x軸上的行進距離，m

Dy2——管段2折角后管段在y軸上的偏移量，m

管段n折角后管段在x軸上的行進距離Dxn及在y軸上的偏移量Dyn的計算式分別為：

DAxn=L(cos q+cos 2q+…+cos nq)    (5)

DAyn=L(sin q+sin 2q+…+sin nq)    (6)

式中Dxn——管段n折角后管段在x軸上的行進距離，m

Dyn——管段n折角后管段在y軸上的偏移量，m

n——管段數量

③管段長度對偏移量的影響

由式(5)、(6)可知，若管段偏移Dyn，則須沿管道初始方向行進Dxn。若在盡量短的行進距離內調整出所需的偏移量，則必須加大實際折角，但根據限制條件——q≤g，q不能無限增大。另一個可變條件是管段長度L，在q不變的條件下，減小L可以縮短達到偏移量所需的行進距離。在實際工程中，單根管子長度一般為12m或6m，為縮短管段長度，可以把整條管子截成若干段短管，一般為6、4、3m等長度。那么，短管的長度是否有限值要求呢?根據CJJ 28—2004《城鎮供熱管網工程施工及驗收規范》第4．2．1條第4款規定：管溝和地上管道兩相鄰環形焊縫中心之間距離應大于鋼管外徑，且不得小于150mm。管溝和地上架空管道應遵守以上條款規定，而對于直埋熱水供熱管道，由于屬于隱蔽工程，出于防泄漏考慮，對管子焊接要求更高，因此至少不應低于以上條款要求。因此，管段的最短長度應大于鋼管外徑且不小于150mm。

以DN 1000mm管道為例，在不同管段長度條件下，對管道在y軸上的偏移量及x軸上的行進距離進行比較。選取以下兩種方案：方案1：管段長度為12m；方案2，管段長度為6m。由文獻[1]可知，在循環溫差為120℃時，最大允許折角g為1.4°，我們就選取實際折角為1.4°作為計算條件。兩種方案的計算結果分別見表1、2。

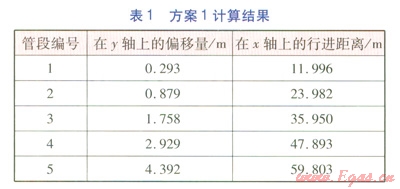
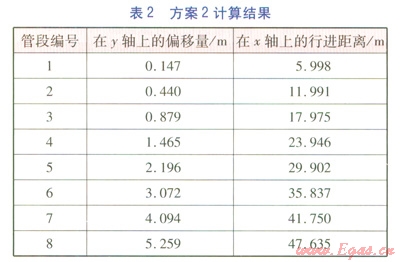
由表1、2可知，若實現0.879m的y軸上的偏移量，方案2在x軸上僅行進17.975m，而方案1需行進23.982m。這說明，采取縮短管段長度的方法，有利于在較短的行進距離內實現較大的偏移量，從而順利避開障礙物。需要指出的是：在實際工程中，我們可以采取多實際折角與多管段長度相結合的處理方法，但焊縫數量不宜過多，以影響施工質量。不應出現避讓開障礙物后，管道調整回原管位時出現實際折角大于最大允許折角的情況。

④算例

某直埋供熱管道規格為DN 1000mm，在敷設過程中遇到障礙物，要求在40m左右的距離內偏移1m，之后管道需再調整回原管位。最大允許折角取1.4°，管段最短長度限定為1m。管道布置方式見圖4。由于管道基本以障礙物(管段8—8¢所在位置)為中心成對稱布置，因此圖4僅給出一側的管道。各節點、各管段的相關計算結果分別見表3、4。為方便表述，定義管段向右側偏轉時，折角為正值；向左側偏轉時，折角為負值。

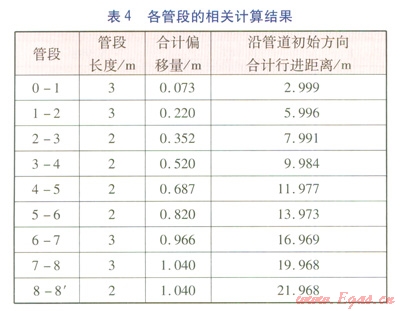
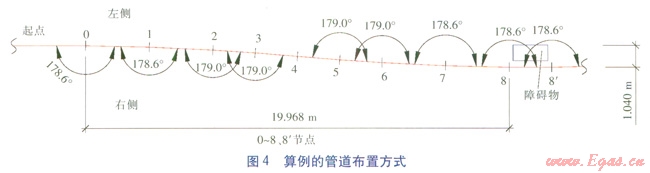
由圖4可知，在節點0位置管段0—1向右側偏轉1.4°，管段1—2、2—3、3—4繼續向右側偏轉，管段4—5不再偏轉(即節點4的折角為0)。隨即，管段5—6向左側偏轉1.0°，管段6—7、7—8、8—8¢繼續向左側偏轉，管段8—8¢為障礙物所在位置并與管道初始方向平行。采取以上布置方式，沿管道初始方向行進19.968m后，整體向右側偏移1.040m，繞過障礙物(即管段8—8¢所在位置)后，繼續行進19.968m重新回到原管位。求解過程中，管段最短長度為2m，最大實際折角為1.4°，滿足限制條件。

3　結語

實際工程中除了平面折角外，也經常出現空間折角，必須求出空間折角的準確值，進而進行應力驗算。在進行多管段連續折角設計時，應靈活確定每段管段的長度及折角，以實現既安全又能避讓障礙物。

參考文獻：

[1]王飛，張建偉．直埋供熱管道工程設計[M]．北京：中國建筑工業出版社，2007：186．

本文作者：趙欣剛  張磊  王冠英  李宏俊

作者單位：中國市政工程華北設計研究總院有限公司第六設計研究院