摘 要:針對分布式能源系統的經濟效益有可能因實際負荷的不確定性無法充分發揮的問題,將考慮設備容量離散性的優化配置方法與最小最大后悔值法相結合,發展了考慮負荷不確定性的魯棒優化配置方法。基于此方法,結合實例,采用由微型燃氣輪機冷熱電三聯供和地下水地源熱泵組成的分布式能源系統形式,研究負荷不確定性對系統配置和經濟性的影響。考慮負荷不確定性有可能改變系統的優化配置容量、設備總造價及年總費用的最大后悔值,并降低系統優化配置方案在實際運行時的經濟風險,使其經濟效益更具魯棒性。該實例研究驗證了該方法的有效性。
關鍵詞:分布式能源系統 負荷不確定性 魯棒優化配置 最小最大后悔值法
Robust Optimization of Distributed Energy System Considering Load Uncertainty
Abstract:The economic benefit of distributed energy system may not be brought into full play due to its actual load uncertainty.Therefore,a robust optimal configuration method considering load uncertainty is developed by combining the optimal configuration method considering discreteness of equipment capacities with the minimax regret criterion.Based on this method,the influence of load uncertainty on the svstein configuration and economy is studied by using the distributed energy system composed of gas microturbinedriven CCHP system and groundwater heat pump.The optimal equipment capacities,the initial investment cost and the maximum regret in annual total cost may change,the economic risk of the optimal configuration scheme of the system during the actual operation can be reduced,and the robustness in the economic benefit is strengthened when the load uncertainty is considered.The validity of the proposed method is verified by the ease study.
Key words:distributed energy system;load uncertainty;robust optimal configuration;minimax regret criterion
1 概述
分布式能源系統(也稱分布式供能系統,Combined Cooling,Heating and Power System,CCHP)是一種臨近用戶設置的發電并結合冷、熱、電聯供等應用拓展的整體能源供應系統。它與電網等集中式能源方式的有機結合是電力工業和能源產業的重要發展方向[1],正日益引起廣泛關注[2-6]。
分布式能源系統的優化配置對于獲得好的經濟效益至關重要,而優化配置又強烈依賴于用戶的各類負荷需求。目前在優化配置中通常采用兩種負荷,一種是夏季、冬季和過渡季等幾種典型日的負荷預測值[7],另一種是全年逐時(8760h)負荷預測值[8]。但前者忽略了同一個季節內負荷的差異;即使是基于后一種方法,現實中存在的氣象條件、內擾不確定性,以及各能量預測供應的對象、面積與實際運行時的偏差,也可能導致聯供系統的設備投資浪費或不足、經濟效益無法充分發揮,極端情況下甚至會出現停運的尷尬局面,上海黃浦區中心醫院就是典型的例證[9]。因此,考慮用戶負荷需求的不確定性,以增強分布式能源系統經濟效益的魯棒性,是聯供系統優化配置的現實需求。
國內外已有學者針對分布式能源系統優化配置中的負荷不確定性開展了初步研究。文獻[10]假定冷熱電負荷值以某種概率密度分布在具有一定不確定度的區間內,并以年總費用的期望值為目標函數,研究了負荷不確定性對常規聯供系統配置和經濟性的影響。文獻[11]在聯供系統優化配置方法中引入最小最大后悔值法,從而在滿足所有可能的負荷需求下,使得聯供系統的年總費用最大后悔值最小化以使其經濟魯棒性最優。但它們均假定設備容量為連續變量,簡化了該優化問題的求解。
目前優化配置方法的前沿是將設備容量作離散化處理,這可以使優化的設備容量與市場上現有設備容量一致,避免了采用連續變量時因按照優化容量就近選擇設備容量而出現經濟效益偏離最優點的情況。但考慮設備容量離散性的系統優化配置是一種典型的混合整數非線性規劃(MINLP)問題,整型變量數目多,求解較為困難。文獻[12]通過增加離散變量的內在約束,較好地解決了這一問題。
本文將考慮設備容量離散性的優化配置方法與最小最大后悔值法相結合,發展了考慮負荷不確定性的魯棒優化配置方法,然后以北京市典型醫院為例,針對由微型燃氣輪機冷熱電三聯供和地下水地源熱泵組成的分布式能源系統,進行了考慮負荷不確定性的魯棒優化配置研究,分析了負荷不確定性對系統配置和經濟性的影響。
2 分布式能源系統的組成
圖1為本文所述分布式能源系統,該系統也稱為復合供能系統[13]。它由微型燃氣輪機、煙氣型溴化鋰機組和地下水地源熱泵等設備組成。以天然氣為燃料的燃氣輪機機組發電用于滿足用戶側電負荷需求,電力不足部分從電網購電補充(根據國內實際情況,規定聯供系統不允許上網售電),電力多余部分可用于驅動地下水地源熱泵機組;燃氣輪機后設置煙氣型溴化鋰機組,利用燃氣輪機產生的高溫煙氣進行制冷或制熱,并聯合地下水地源熱泵機組共同滿足用戶側冷(熱)負荷需求。其中,地下水地源熱泵夏季制冷、冬季制熱,可通過四通換向閥改變冷媒的流向來實現,在制冷工況下,室內熱交換器就是蒸發器,室外熱交換器就是冷凝器;在制熱工況下,室內熱交換器就是冷凝器,室外熱交換器就是蒸發器。
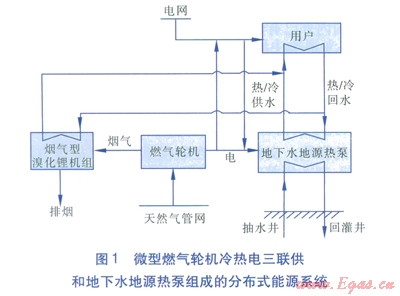
將微型燃氣輪機冷熱電三聯供與性能系數高、部分負荷性能好的地下水地源熱泵相結合,可降低CCHP系統的電熱產出比,緩解其所發多余電力不能上網的約束,提高系統運行靈活性;相對于單獨的地下水地源熱泵系統,地下抽水量少(受水資源量限制小)。
3 考慮設備容量離散性的優化配置
3.1 能源系統單元部件模型
3.1.1燃氣輪機
燃氣輪機的性能受負荷和環境空氣溫度的影響較大,而且輸出電功率也有一定的范圍,建模時充分考慮了以上因素。

式中Pgt——燃氣輪機的輸出電功率,kW
q——燃氣輪機工作的環境空氣溫度,℃
P1、q1、P2、q2——系數,是環境空氣溫度的函數
Fgt,f——燃氣輪機消耗的燃料熱功率,kW
dgt——燃氣輪機的狀態參數,運行時為l,停機時為0
a1、b1、c1、d1、a2、b2、c2、d2、k1、k2——無量綱系數,與燃氣輪機的型號有關
Fgt——燃氣輪機排煙中可供利用的余熱熱功率,kW
Fgt,f,max——燃氣輪機滿負荷時消耗的燃料熱功率,kW
Fgt0,f,max——設計工況環境空氣溫度下燃氣輪機滿負荷時消耗的燃料熱功率,kW
q0——燃氣輪機設計工況下的環境空氣溫度,℃
Fgt,f,min——燃氣輪機輸出電功率下限時消耗的燃料熱功率,kW
3.1.2煙氣型溴化鋰機組
考慮機組輸出功率的上下限,并假定機組性能系數(hCOP,ac)保持不變,采用如下模型:
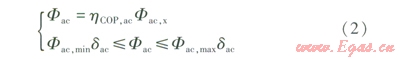
式中Fac——煙氣型溴化鋰機組的制冷(熱)功率,kW
hCOP,ac——煙氣型溴化鋰機組的制冷(熱)性能系數
Fac,x——煙氣型溴化鋰機組從煙氣中回收的余熱熱功率,kW
Fac,min——煙氣型溴化鋰機組的最小制冷(熱)功率,kW
dac——煙氣型溴化鋰機組的狀態參數,運行時為l,停機時為0
Fac,max——煙氣型溴化鋰機組的最大制冷(熱)功率,kW
3.1.3地下水地源熱泵機組
考慮機組輸出功率的上下限,并假定機組性能系數(hCOP,gwhp)保持不變,采用如下模型:
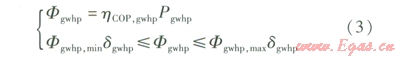
式中Fgwhp——地下水地源熱泵機組的制冷(熱)功率,kW
hCOP,gwhp——地下水地源熱泵機組的制冷(熱)性能系數
Pgwhp——地下水地源熱泵機組的耗電功率,kW
Fgwhp,min——地下水地源熱泵機組的最小制冷(熱)功率,kW
dgwhp——地下水地源熱泵機組的狀態參數,運行時為l,停機時為0
Fgwhp,max——地下水地源熱泵機組的最大制冷(熱)功率,kW
3.2 優化運行的目標函數和約束條件
3.2.1目標函數
在滿足給定的冷熱電負荷的條件下,優化運行的目標函數取某一時間段內整個系統的運行能耗費用,即系統消耗天然氣的支出與從電網購電的支出之和:
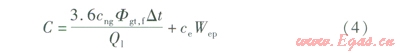
式中C——某一時間段內整個系統的運行能耗費用,元
Cng——天然氣價格,元/m3
Dt——系統運行的時間長度,h,取lh
Q1——天然氣低熱值,MJ/m3
Ce——購電價格,元/(kW·h)
Wep——該時間段內系統購電量,kW·h
3.2.2約束條件
優化運行的約束條件分為兩部分:一部分即各設備的運行特性和負荷率約束,如式(1)~(3)所示;另一部分為聯供系統各能流平衡約束,如式(5)~(7)所示。
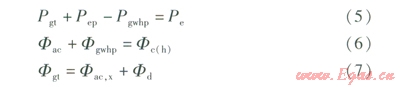
式中Pep——系統購電功率,kW
Pe——用戶側除地下水地源熱泵機組外的用電負荷,kW
Fc(h)——用戶側冷(熱)負荷,kW
Fd——排煙中廢棄的可供利用余熱熱功率,kW
3.3 優化配置
聯供系統優化配置問題的求解分為上下兩層:下層求解確定配置的優化運行問題,得到該配置下系統的最低運行能耗費用;上層求解考慮設備容量離散性的優化配置問題,最終從各種組合方案中選出年總費用最小的配置方案。
聯供系統的優化配置以年總費用為目標函數,包括年運行能耗費用和初投資年等值費用兩部分。其中,年運行能耗費用是指系統全年消耗的天然氣和從電網購電產生的費用;初投資年等值費用是指各設備總投資根據使用年限折合到每年的平均投資。可用下式表示:
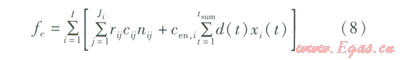
式中¦c——年總費用,元
i——系統選用的設備種類
I——系統選用的設備種類上限,本文為3
j——設備可供選擇的型號號數
Ji——第i種設備可供選擇的型號數
rij——第i種j型號設備的資本回收系數
Cij——第i種j型號設備的造價,元
nij——第i種j型號設備的被選臺數
Cen,i——第種設備所消耗能源的價格,電價,元/(kW·h),氣價,元/m3
t——典型日的時段,本文中夏季、冬季、過渡季典型日均分為24個時段,每個時段長度為1h
tsum——三種典型日的時段數之和
d——全年各種典型日的持續天數,d
xi——第i種設備每個時段消耗能源的量,電量,kW·h,天然氣量,m3
在對聯供系統進行優化配置時,若考慮設備容量的離散性,將使整型變量數目增多,進而增大問題的求解難度。為解決此問題,可以增加離散變量的內在約束,具體如下式所示[12]:

式中Nij——第i種,型號設備最多可選臺數
¡ij——第i種,型號設備是否選擇,選擇為1,不選為0
式(1)~(9)組成了此分布式能源系統優化配置的混合整數非線性規劃(MINLP)模型。該模型考慮了設備的運行特性(如部分負荷率和環境空氣溫度對燃氣輪機性能的影響、設備輸出功率范圍的限制等),在方案優選階段即可實現設備容量的離散及優化,從而實現了分布式能源系統的全工況優化配置。
4 基于最小最大后悔值法的魯棒優化配置
4.1 基本概念
數學規劃的經典范例是在輸入數據準確知道并且等于某些標稱值的假設條件下建立模型,并利用已有的數學規劃求解方法得到最優解。這種方法沒有考慮數據不確定性的影響,故當數據的取值不同于標稱值時,原來得到的最優解可能不再最優甚至變得不可行。因此,需要找到一種優化方法使優化解受數據不確定性的影響最小,這種方法就是魯棒優化方法。
為使分布式能源系統的優化配置方案在實際運行時的經濟效益更具魯棒性,本文通過引入最小最大后悔值法來減小負荷不確定性對系統配置和經濟性的影響。最小最大后悔值法是一種決策分析方法,其目的就是要選擇一種方案,使得負荷由于最小可能值、預測值和最大可能值3種自然狀態所體現出來的不確定性對配置方案在實際運行時帶來的損失最小。其中,后悔值定義為非優化配置方案與優化配置方案的目標函數(本文中為年總費用)之間的差額。
決策分析方法不止一種,但如果是一次性的投資決策,而且對未來把握比較小,要求穩妥行事的場合,采用最小最大后悔值法比較合適。
4.2 最小最大后悔值法的實現步驟
最小最大后悔值法的決策步驟通常分為四步,就本文而言,它們是:
第一步,優化得到各種方案在不同自然狀態下的年總費用,并確定各種自然狀態下年總費用最小的方案;
第二步,把各種情況下的年總費用減去相應自然狀態下的最小年總費用,求得后悔值;
第三步,找出各種方案在不同自然狀態下的最大后悔值;
第四步,在已確定的各最大后悔值中找出最小的最大后悔值,對應方案即為最優方案。
在這里,為描述不確定性負荷的3種自然狀態,引入負荷不確定度的概念,其定義為負荷的實際值偏離預測值的百分比。假定負荷的最小、最大可能值偏離預測值的比例相等,則負荷的可行域可表示為[14]:
(1-a)gA≤g≤(1+a)gA (10)
式中a——負荷不確定度
gA——負荷的預測值,kW
g——負荷的實際值,kW
基于考慮設備容量離散性的優化配置方法,在引入最小最大后悔值法后,分布式能源系統魯棒優化配置的具體求解流程如表l~2所示。
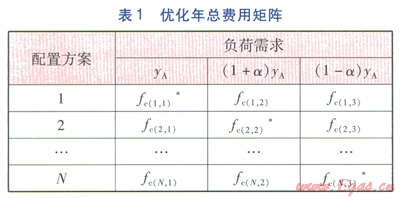
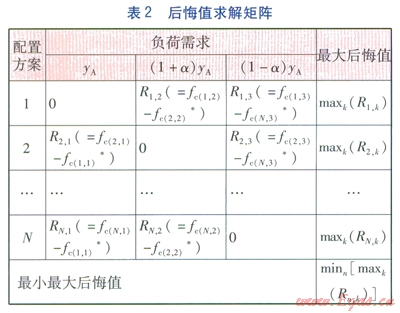
表1是由各種配置方案在3種不同負荷需求下優化得到的年總費用所構成的矩陣。“*”表示在某種負荷需求下,該方案的年總費用最小。
表2實現了4.2節所述的第二、三、四步。其中,后悔值用R表示。因此,與最小最大后悔值minn[maxk(Rn,k)]所對應的方案即為考慮負荷不確定性后分布式能源系統的優化方案。
5 算例研究
5.1 建筑負荷
以北京市某3×104m2的典型醫院為例進行分析。將全年分為夏季(100d)、冬季(125d)和過渡季(60d)3種情況,每種情況以1個典型日為代表,在優化計算時僅考慮冷(熱)負荷和電負荷,不考慮熱水或蒸汽負荷,且系統中不考慮設備補燃方式。需要說明的是,在除上述3種情況外的剩余天數中,能源供應不考慮聯供方式。
假定冷、熱、電負荷的最小、最大可能值偏離預測值的比例相等,則醫院各季節典型日的逐時不確定性負荷曲線如圖2、3所示。其中,實線代表負荷的預測值,gA,c(h)表示冷(熱)負荷的預測值,gA,e表示電負荷的預測值,而由實線上下各偏移a所圍成的區域即為負荷的可行域。
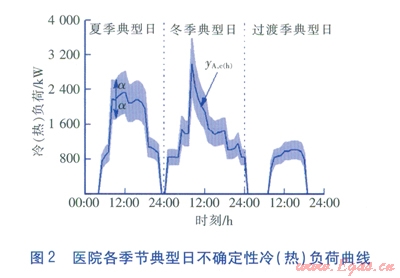
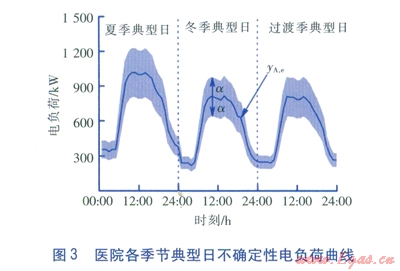
該醫院的峰值負荷及全年能耗匯總見表3。

5.2 計算參數及工況
系統可供選擇的設備參數見表4。在計算中,貸款年利率取5.94%,設備的使用年限統一取l5a。分時電價為:10:00~15:00、18:00~21:00為峰段,電價l.0125元/(kW·h);23:00~7:00為谷段,電價0.3535元(kW·h);7:00—10:00、15:00~18:00、21:00~23:00為平段,電價0.6725元/(kW·h)。氣價取l.85元/m3,天然氣低熱值取35.2 MJ/m3。燃氣輪機模型中的系數取值見文獻
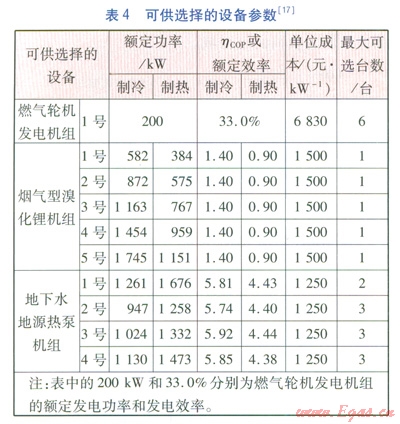
本文所述分布式能源系統包括3種主要設備,即設備種類上限I為3;發電設備選取單機容量為200kW的微型燃氣輪機發電機組,即型號數J1為1,依據該醫院的負荷特性,限制其可選臺數為l~6臺;根據不同臺數發電設備的排煙可利用熱量,選取5種(即型號數J2=5)不同型號的煙氣型溴化鋰機組,每種型號最多可選l臺;地下水地源熱泵機組的容量考慮極限工況,即在發電設備和煙氣型溴化鋰機組不運行時,地下水地源熱泵機組也能滿足用戶的最大冷、熱負荷需求,其可選型號數J3為4,每種型號可選2~3臺。
為了考察負荷不確定性的影響,計算如下5個工況的優化配置:
工況l:不考慮負荷的不確定性,即a=0%;
工況2~5:冷熱電負荷的不確定度a分別為10%、20%、30%和40%。
相應地,為了與工況2~5相匹配,地下水地源熱泵機組的容量考慮了4種實際型號。
5.3 優化配置結果及分析
假定在“以熱定電,并網不上網”的運行原則下,計算得到上述5種工況下的優化配置結果,見表5。
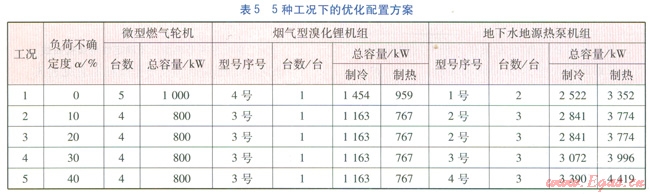
由表5可以看出,在傳統的不考慮負荷不確定性的優化配置結果中,即在工況l下,發電機組臺數為5臺;而在考慮負荷具有l0%~40%不確定度時,優化配置程序給出的發電機組臺數為4臺;煙氣型溴化鋰機組的容量與燃氣輪機排煙中的可利用余熱量有關,地下水地源熱泵機組的容量因考慮極限工況而與最大冷、熱負荷有關。
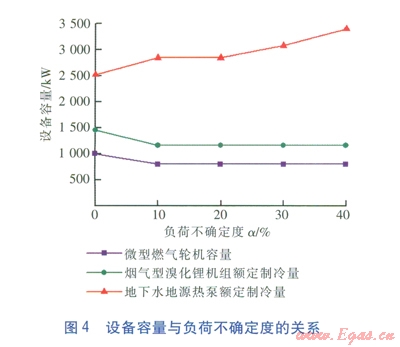
在上述5種工況的優化配置方案中,各種設備的優化容量與負荷不確定度的具體關系見圖4,其中,溴化鋰機組和熱泵機組僅給出了額定制冷量。由圖4可以看出,隨著負荷不確定度a的增加,地下水地源熱泵機組的額定制冷量因考慮極限工況而逐漸增大,而微型燃氣輪機發電機組和煙氣型溴化鋰機組的容量在考慮負荷不確定性后反而有所減小。這是因為魯棒優化配置避免了在負荷需求偏小時出現由于所有設備容量均增大而引起的年總費用后悔值增大的情況,從而降低了系統的優化配置方案在實際運行時的經濟風險,使其更具經濟魯棒性。
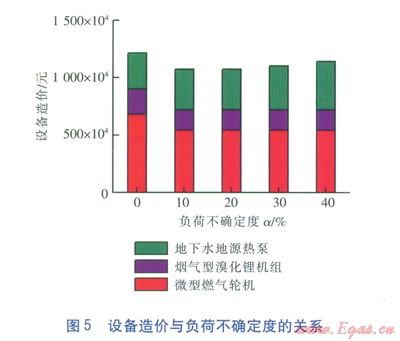
5種工況下相應優化配置方案的設備造價情況見圖5。可以看出,發電機組的造價在系統初投資中占較大比例;由于分布式能源系統的優化配置在考慮負荷不確定性后,發電機組的臺數由5臺減為4臺,因此,系統的初投資相對于傳統的不考慮負荷不確定性的優化配置方案而言有所減少;隨著負荷不確定度的增加,地下水地源熱泵機組的造價因考慮極限工況而增加,使得總的初投資逐漸增加。
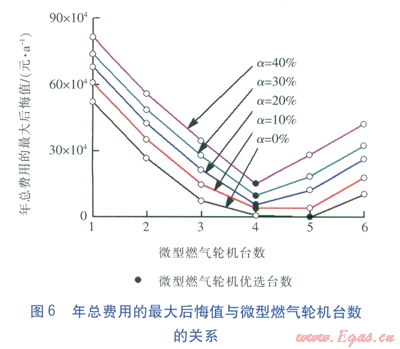
通過對5種工況下各種方案的優化運行結果進行分析,得到在不同負荷不確定度下,年總費用的最大后悔值與發電機組臺數的關系,見圖6。可以看出,在不考慮負荷不確定性的工況1下,最大后悔值最小的方案(最優方案)所對應的發電機組臺數為5臺;當考慮實際運行中存在的負荷不確定性后(工況2~5),最優方案的燃氣輪機臺數變為4臺,此時,配置5臺發電機組的方案其經濟魯棒性反而較差。這說明傳統的不考慮負荷不確定性的優化配置方案在實際運行時的經濟魯棒性可能并非最佳,從而印證了在分布式能源系統優化配置中考慮負荷不確定性的必要性。
6 結論
本文將考慮設備容量離散性的優化配置方法與最小最大后悔值法相結合,發展了考慮負荷不確定性的魯棒優化配置方法。其實質就是在初投資最少與年運行能耗費用最小之間找到平衡點,使得兩者之和(即評價經濟性最優的年總費用指標)受負荷不確定性的影響最小化。這樣,既避免了按單一的最大或最小負荷配置系統時出現設備容量偏大或偏小的問題,降低了負荷不確定性給系統的優化配置方案在實際運行時帶來的經濟風險,保證了經濟效益能得到充分發揮,又使得優化的設備容量與市場上現有設備的容量一致,避免了采用連續變量時因按照優化容量就近選擇設備容量而出現經濟效益偏離最優點的情況。此方法可為分布式能源系統的合理配置提供參考。
參考文獻:
[1]杜建一,王云,徐建中.分布式能源系統與微型燃氣輪機的發展與應用[J].工程熱物理學報,2004,25(5):786-788.
[2]段潔儀,馮繼蓓,梁永健.樓宇式天然氣熱電冷聯供技術及應用[J].煤氣與熱力,2003,23(6):337-341.
[3]馮繼蓓,高峻,楊杰,等.樓宇式天然氣冷熱電聯供技術在北京的應用[J].煤氣與熱力,2009,29(3):Al0-Al3.
[4]胡小堅,王忠平,張雪梅,等.分布式天然氣CCHP系統應用研究現狀與前景[J].煤氣與熱力,2011,31(4):A04-A09.
[5]張云飛.杭州市推廣天然氣熱電冷聯供系統的可行性[J].煤氣與熱力,2007,27(2):67-69.
[6]王振興,喬艷麗.天然氣CHP、CCHP系統在工業企業的應用[J].煤氣與熱力,2011,31(12):Al5-A18
[7]黃興華,李贊.聯供系統設備配置與運行策略集成優化研究[J].太陽能學報,2008,29(1):24-28.
[8]PIACENTINO A,CARDONA F.On thermoeconomics of energy systems at variable load conditions:Integrated optimization of plant design and operation[J].Energy Conversion and Management,2007,48(8):2341-2355.
[9]劉麗紅,袁益超,劉聿拯.分布式能源的現狀與發展[J].熱力發電,2006,35(8):4-7.
[10]李朝振,石玉美,黃興華.負荷不確定性對三聯供系統配置和經濟性的影響[J].暖通空調,2009,39(7):13-17.
[11]YOKOYAMA R,ITO K.Robust optimal design ot’a gas turbine eogeneration plant based on minimax regret eriterion[C]//American Society of Mechanical Engineers.44th ASME Gas Turbine and Aeroengine Technical Congress,Exposition and Users Symposium.New York(USA):ASME Press,1999:1-8.
[12]YOKOYAMA R,ITO K.Optimal design of gas turbine cogeneration plants in consideration of discreteness of equipment capabilities[J].Journal of Engineering for Gas Turbines and Power,2006,128(2):336-343.
[13]林怡,張士杰,肖云漢.復合供能系統優化配置和運行策略研究[J].暖通空調,2011,41(10):84-90.
[14]YOKOYAMA R,ITO K.Optimal design of energy supply systems based on relative robustness criterion[J].Energy Conversion and Management,2002,43(4):499-514.
[15]MAVROTAS G,DIAKOULAKI D.FLORIOS K.et al.A mathematical programming framework for energy planning in services’sector buildings under uncertainty in load demand:The case of a hospital in Athens[J].Energy Policy,2008,36(7):2415-2429.
[16]林怡.微小燃機熱電冷聯供與地下水源熱泵耦合系統研究(碩士學位論文)[D].北京:中國科學院研究生院(工程熱物理研究所),2010:13.
[17]劉愛國,張士杰,肖云漢.微燃機與小燃機在南方地區分布式聯供系統中的應用比較[J].燃氣輪機技術,2009,22(3):1-9.
本文作者:林怡 張士杰 肖云漢
作者單位:北京市燃氣集團研究院
中國科學院先進能源動力重點實驗室(工程熱物理研究所)
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助
