泡沫鉆井環空巖屑濃度影響因素分析

摘 要

摘要：為了準確地計算泡沫鉆井環空巖屑濃度，利用多相流體力學方法計算了該值，并著重分析和討論了巖屑直徑、巖屑形狀和注液流量對其的影響，建立了泡沫鉆井過程中泡沫、巖屑在環空
摘要：為了準確地計算泡沫鉆井環空巖屑濃度，利用多相流體力學方法計算了該值，并著重分析和討論了巖屑直徑、巖屑形狀和注液流量對其的影響，建立了泡沫鉆井過程中泡沫、巖屑在環空中流動的數學模型，還采用修正Simple方法對該模型進行了數值求解。計算結果表明：①巖屑顆粒直徑越大，環空巖屑濃度越大；②巖屑形狀越不規則，環空巖屑濃度越低；③在淺井段，環空巖屑濃度隨注液流量的增大而增大，而在深井段，環空巖屑濃度隨注液流量的增大而增大；④該數學模型考慮了加速度和泡沫與巖屑之間相對滑動的影響，預測的井底壓力更接近于實驗數據，計算的環空巖屑濃度更準確。
關鍵詞：泡沫鉆井；環空巖屑濃度；巖屑形狀；巖屑直徑；注液流量；應用效果
0 引言
   由于泡沫鉆井液具有攜帶巖屑能力強和在欠壓實地層鉆進不會沖蝕井眼等優點，主要用來鉆穿含水地層、漏失嚴重地層和地層傷害敏感產層的深井，從20世紀90年代以來得到了迅速的發展[1]。對于泡沫鉆井，能否準確地預測井底壓力，對安全鉆井和保護儲層非常重要。影響井底壓力的主要因素有：井口回壓、注液流量、注氣流量、地層流體侵入、鉆速、巖屑尺寸和巖屑形狀。其中巖屑主要通過對重力和摩擦力來影響井底壓力。因此，如何準確地計算環空巖屑濃度對預測井底壓力的準確性至關重要。國內外對泡沫攜帶巖屑規律做了大量的理論和實驗研究[2～4]，在這些理論研究中，將泡沫和巖屑看作混合物，巖屑按照等直徑的球形顆粒來處理，利用經驗公式計算巖屑濃度。另外，王利國[5]研究了穩定泡沫鉆水平井井筒穩定流動。筆者則采用泡沫-巖屑兩相流力學方法研究泡沫在直井中攜帶巖屑的規律，通過求解多相流方程來確定環空巖屑濃度，另外還分析了巖屑直徑和形狀、注液流量對巖屑濃度的影響。
1 數學模型
    筆者的研究基于如下假設：①泡沫和巖屑在垂直環空中為一維穩定流動，地層流體穩定侵入，不影響氣泡在液相中的分散性；②泡沫黏度滿足冪律流變模式，采用Kuru[6]給出的公式計算泡沫的稠度系數和流性指數；③巖屑顆粒大小相同，均勻分散在泡沫中，忽略巖屑顆粒之間和巖屑顆粒與井筒的相互作用的影響；④環空中泡沫溫度與地層溫度相同，且與井深呈線性關系。
1.1 連續性方程
由假設條件可知，泡沫和巖屑在環空中流動的連續性方程為：
 
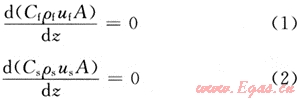
式中：Cf、Cs分別為泡沫和巖屑濃度，無因次；ρf、ρs分別為泡沫和巖屑密度，kg/m3；μf和μs分別為泡沫和巖屑流動速度，m/s；A為環空橫截面積，m2。
1.2 動量方程
    由液固兩相流體力學[6]可得泡沫和巖屑在環空中一維穩定流動的動量方程分別為：
 
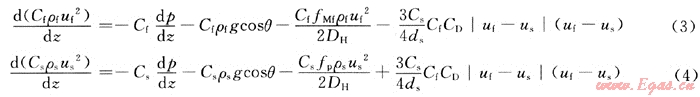
式中：p為壓力，Pa；θ為井斜角，(°)；fMf、fp分別為泡沫和巖屑的摩擦系數，無因次；DH為環空水力直徑，m；ds為巖屑直徑，m；CD為巖屑顆粒的拖曳力系數，無因次。
    泡沫和巖屑摩擦系數的計算非常重要，本文參考文獻[6]給出了泡沫在環空中層流和紊流時的摩擦系數計算公式；本文參考文獻[7～9]給出了計算巖屑顆粒的拖曳力系數和摩擦系數的計算公式。
1.3 氣體狀態方程
泡沫中的氣相不是理想氣體，采用非理想氣體狀態方程描述壓力、溫度和氣體密度之間的關系：
 
式中：ρg為泡沫氣相密度，kg/m3；Mg為泡沫氣相摩爾質量，kg/kmol；Z為氣體壓縮系數，無因次；R為氣體常數，這里取8314J/(kmol·K)；T為溫度，K。
1.4 邊界條件
泡沫在直井中攜帶巖屑的邊界條件為：①環空出口處的壓力已知；②井底處泡沫的質量流量；③井底處的巖屑濃度采用式(6)計算。
 
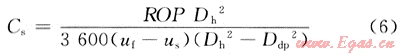
式中：ROP為機械鉆速，m/h；Dh和Ddp分別為井眼徑和鉆桿外徑，m。
2 數學模型的數值求解
    通過對不同鉆井工況下泡沫在環空中的流動研究可知，馬赫數在井口處最大，約為0.01，沒有達到可壓縮流動的條件。因此，這里將泡沫-巖屑兩相流看作變密度流體-固體顆粒兩相流，具體的數值求解方法為：①在交錯網格上將連續性方程和動量離散；②采用李國美等人的修正simple(速度、濃度、壓力修正)方法[10]求解離散方程；③編制相應的求解程序。
3 算例與結果分析
    計算時所需的基本數據如下：井口回壓(pb)為414kPa；控制體數目(N)為1000；井深(H)為1500m；井眼直徑(Dh)為O.2m；鉆桿外徑(Ddp)為0.11m；巖屑顆粒直徑(ds)為0.013m；巖屑密度(ps)為2700kg/m3；巖屑形狀系數為1；地面溫度為16℃；地溫梯度為0.003K/m；鉆速為18.3m/h；注氣流量為17.5m3/min；注液流量為150L/min；泡沫由水、空氣和發泡劑組成。地層流體侵入流量為13L/min。
    采用Okpobiri方法[2]預測的井底壓力比實驗數據平均大9.11%左右。但由于文獻中沒有原始實驗數據，為了驗證本文計算模型的準確性，只能分別采用多相流方程和Okpobiri方法計算的井底壓力進行對比，表1給出了不同鉆井參數條件下井底壓力的對比結果。從表1可知，Okpobiri方法計算的井底壓力比本文模型平均大6.78%，所以認為本文建立的數學模型預測壓力更接近于實驗數據。這主要是因為：①多相流動量方程考慮了加速度的影響，由于隨著井深的增加，泡沫和巖屑的流速減小，所以加速壓降是負值，總壓降隨之減小；②當巖屑濃度相同、泡沫質量、密度和流速相同時，Okpobiri方法計算的摩擦壓降偏大。另外，Okpobiri方法假設泡沫和巖屑沒有滑移速度，即泡沫和巖屑速度相等，采用Okpobiri方法計算的巖屑濃度比采用多相流方程計算的巖屑濃度低。事實上，泡沫和巖屑之間存在相對滑移，所以采用多相流方程計算的環空巖屑濃度更準確。
表1 井底壓力對比表
基本數據
Okpobiri方法
本文模型
對比誤差/%
井深/m
鉆速/m·h-1
井口回壓/kPa
注氣流量/m3·min-1
注液流量/L·min-1
井底壓力/kPa
井底壓力/kPa
3.5
18.3
276
6.5
91
1136.8
1067.0
6.54
500
18.3
276
9.6
136
1876.3
1753.2
7.02
1000
18.3
276
11.7
170
4249.7
3984.0
6.67
1500
18.3
414
13.6
159
6846.1
6228.2
6.71
305
27.4
138
5.0
136
1228.6
1106.2
6.77
500
27.4
276
10.0
136
1967.4
1800.0
6.93
1000
27.4
276
12.1
170
4437.6
4155.8
6.78
1500
27.4
414
17.5
163
6738.5
6306.7
6.85
   

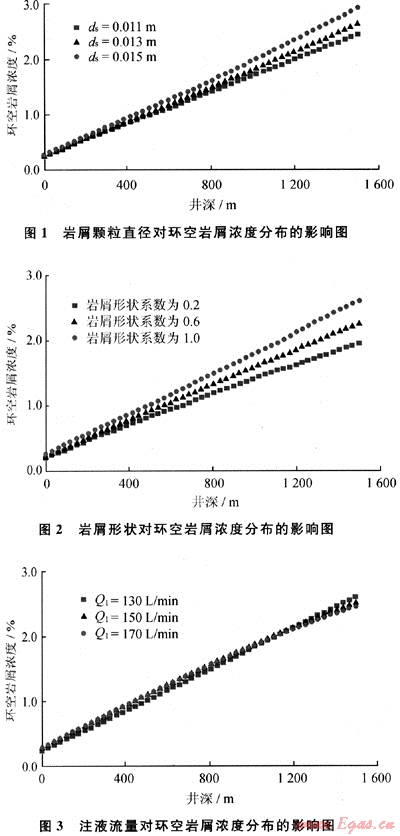
　　由圖1～3可知：隨著井深的增加，環空巖屑濃度隨之增大，在井底處環空巖屑濃度最大。這是因為環空中的壓力隨井深的增加而增加，壓力使泡沫質量和流速減小，降低了泡沫攜帶巖屑能力，所以巖屑沉降速度增大，巖屑濃度增大；由圖1可知：巖屑顆粒直徑越大，環空巖屑濃度隨之增大，這是因為，巖屑顆粒直徑的增大使泡沫與巖屑之間的滑移速度變大，即巖屑的流動速度降低，所以巖屑濃度增大。由于鉆井過程中產生的巖屑顆粒直徑并不完全相等，若假設巖屑顆粒直徑相同，會對計算結果產生一定的誤差。
    由圖2可知：巖屑形狀越不規則，即形狀系數越小，環空巖屑濃度越低。這是因為，巖屑形狀越不規則，泡沫對巖屑顆粒的拖曳力越大，巖屑顆粒的沉降速度減小，所以環空巖屑濃度降低。實際上巖屑不是球形的，若假設巖屑形狀系數為1，計算的環空巖屑濃度偏小，巖屑形狀系數一般取0.7924[7]。
    由圖3可知：在其他參數相同的情況下，隨著注液流量的增大，在淺井段環空巖屑濃度增大，在深井段環空巖屑濃度減少，即在淺井段泡沫的攜帶巖屑能力下降，而深井段泡沫攜帶巖屑能力提高。這是因為隨著注液流量的增大，泡沫質量減小，當泡沫質量大于0.915時，隨著泡沫質量的減小，泡沫的稠度系數減小、流性指數增大、泡沫黏度降低，在淺井段泡沫質量一般為0.915～0.96，所以在淺井段隨著注液流量增大，泡沫攜帶巖屑能力降低，環空巖屑濃度增大；但當泡沫質量小于0.915時，隨著泡沫質量的減小，黏度的增大、流性指數減小、泡沫黏度增大，在深井段泡沫質量一般為0.55～0.915，所以在深井段隨著注液流量增大，泡沫攜帶巖屑能力增強，環空巖屑濃度降低。從前面的分析可知，在泡沫鉆井過程中，泡沫質量是影響泡沫攜帶巖屑能力的主要因素。另外泡沫質量還對泡沫的穩定性和井底壓力影響比較大，所以說對于泡沫鉆井，對泡沫質量的控制非常關鍵，通常通過調節井口回壓、注液流量和注氣流量來實現[2]。
4 結論
1) 筆者建立的泡沫、巖屑流動的數學模型考慮了加速度和泡沫與巖屑之間相對滑動的影響，可準確地計算環空巖屑濃度，預測的井底壓力更接近實驗數據。
2) 巖屑顆粒直徑、巖屑尺寸和注液流量對環空巖屑濃度影響比較大，若要對環空巖屑濃度計算的更準確，需對鉆井產生的巖屑進行統計分析，得到準確的平均巖屑顆粒直徑和形狀系數。
    3) 泡沫質量是影響泡沫攜帶巖屑能力的主要因素，可通過調節井口回壓、注液流量和注氣流量來控制泡沫質量的范圍。以本文建立的泡沫、巖屑流動數學模型為基礎，可對井口回壓、注液流量和注氣流量等泡沫鉆井水力參數進行優化設計。
參考文獻
[1] GUO B，GHALAMBOR A.欠平衡鉆井氣體體積流量的計算[M].北京：中國石化出版社，2006.
[2] 0KPOBIRI，GODWIN A，IKOKU，et al. Volumetric requirements for foam and mist drilling operations[J].SPE Drilling Engineering，1986，1(1)：71-88.
[3] HERZHAFT B，TOURE A，BRUNI F，et al. Aqueous foams for underbalanced drilling：the question of solids[C]∥SPE Annual Technical Conference and Exhibition. Dallas，Texas：SPE，2000.
[4] MASUDA Y，DOAN Q，OGUZTORELIF M，et al. Critical cuttings transport velocity in inclined annulus：experimental studies and numerical simulation [C]∥SPE/CIM International Conference on Horizontal Well Technology. Calgary，Alberta，Canada：SPE，2000.
[5] 王利國，楊虎，許期聰，等.穩定泡沫鉆井水平井井筒穩定流動的解析模型[J].天然氣工業，2008，28(6)：90-92.
[6] KURU E，OKUNSEBOR O M，LI Y. Hydraulic optimization of foam drilling for maximum drilling rate in vertical wells[J].SPE Drilling 8L Completion，2005，20(4)：258-267.
[7] CHIEN SZE-FOO. Settling velocity of irregularly shaped particles[J].SPE Drilling & Completion，1994，9(4)：281-289.
[8] INDRA GUNAWAN，RUDI RUBIANDINI. Determining cutting transport parameter in a horizontal coiled tubing underbalanced drilling operation[C]∥SPE Asia Pacific Oil and Gas Conference and Exhibition. Melbourne，Australia：SPE，2002.
[9] 龐東豪，袁騏驥.空氣鉆井攜巖及防爆最小注氣量計算方法[J].天然氣工業，2009，29(3)：62-64.
[10] 李國美，王躍社，孫虎，等.節流器內液-固兩相流固體顆粒沖蝕數值模擬[J].石油學報，2009，29(1)：145-148.
 
(本文作者：王長江 中國石油大學石油天然氣工程學院 北京)