蒸汽管道暖管過程管道對固定支座的沖擊

摘 要

摘要：蒸汽管道暖管時，由于管道熱膨脹引起管道由靜止突然發生運動，使管道對固定支座產生沖擊力。應用理論力學中動力學理論分析了沖擊力產生的原因，推導出理論公式。提出彈性固定
摘要：蒸汽管道暖管時，由于管道熱膨脹引起管道由靜止突然發生運動，使管道對固定支座產生沖擊力。應用理論力學中動力學理論分析了沖擊力產生的原因，推導出理論公式。提出彈性固定支座的設計理論，給出了在暖管過程中能保證固定支座安全可靠的彈性系數計算式。
關鍵詞：蒸汽管道；暖管；彈性固定支座；沖擊力
Impact of Pipeline to Fixed Support during Warming Steam Pipeline
WANG YU-xuan，GA0 Bai-zheng，LIU De-ping
Abstract：When warming steam pipeline，the pipeline moves suddenly from a static state to produce an impact force to the fixed support because of pipeline thermal expansion. The reasons for the impact force are analyzed by kinetic theory in theoretical mechanics，and the theoretical formula is derived. The design theory of elastic fixed support is put forward，and the calculation formula of elastic coefficient that can ensure the safety and reliability of the fixed support during warming pipe is given.
Key words：steam pipeline；warming pipe；elastic fixed support；impact force
1 概述
    “蒸汽管道在冷態啟動時必須進行暖管，暖管速度不宜過快”，這是蒸汽管道運行的常識[1、2]。原因在于，若暖管速度過快，易造成管道振動，破壞固定支座。也有人認為：若暖管速度過快，凝結水還未來得及排出，易造成水擊，從而造成管道振動。筆者認為：僅從水擊方面考慮，未必需要緩慢暖管。若采用過熱蒸汽吹掃管道，直接快速打開首端閥門，少量凝結水與高速蒸汽混合，形成霧狀汽水兩相流，不易造成水擊。經分析，溫變時蒸汽管道熱伸長運動的動能，是暖管時引起管道振動的動力源。本文對蒸汽管道暖管過程中管道對固定支座的沖擊進行分析。
2 暖管動力學分析
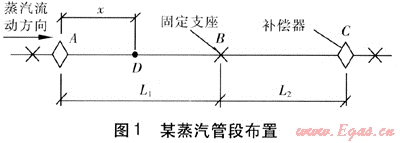
    某蒸汽管段布置見圖1。長度為L1、L2的兩段直管段，設置3個固定支座和兩個波紋管補償器A、C。設暖管前鋼管溫度為θ1、暖管蒸汽溫度為θ2、管道單位長度質量為ml。蒸汽由A端進入，流速為v。與直徑相比，鋼管的壁厚較小，且鋼材的熱導率較大，忽略管壁的溫升過程，即按蒸汽到達之處管壁溫度與蒸汽溫度相同考慮。當暖管蒸汽到達點A，并從點A繼續向前流動一段距離菇到達點D時，管段AD伸長量的計算式為：
    r=xαl(θ2-θ1)    (1)
    x=vt              (2)
式中r——管段AD的伸長量，m
    x——暖管蒸汽由點A向前流動的距離，m
    αl——鋼管的線脹系數，K-1
    θ2——暖管蒸汽溫度，℃
    θ1——暖管前鋼管溫度，℃
    v——暖管蒸汽流速，m/s
    t——蒸汽由點A流動至點D需要的時間，s
    將式(2)代入式(1)得：
    r=vtαl (θ2-θ1)    (3)
以時間t為變量，對式(3)求一階導數，可得到由于管段AD熱伸長，引起管段AD相對于管段DC的運動速度：
 
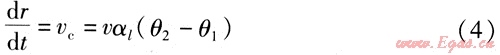
式中vc——由于管段AD的熱伸長，引起管段AD相對與管段DC的運動速度，m/s
    在暖管時，設管段AD在點D膨脹產生速度v1，必然有一個瞬間反作用力，相當于管段AD與管段DC在點D發生彈性碰撞。設彈性碰撞前管段DC的速度為v2，完全彈性碰撞后管段AC的速度為v0，根據完全彈性碰撞的動量守恒定律[3]，得：
    mlxv1+mlv2(L1+L2-x)=mlv0(L1+L2)    (5)
式中ml——管道單位長度質量，kg/m
    v1——管段AD在點D膨脹產生的速度，m/s
    v2——彈性碰撞前管段DC的速度，m/s
    L1——管段AB的長度，m
    L2——管段BC的長度，m
    v0——完全彈性碰撞后管段AC的速度，m/s
   令L1+L2=L，式(5)可以寫成：
    x(v1-v2)+Lv2=Lv0    (6)
式中L——管段AB、BC的總長度，m
    由于v2與v1方向相反，因此有：
    vc=v1+v2    (7)
   將式(7)代入式(4)，并令θ2-θ1=θ，得：
    v1+v2=vαlθ    (8)
式中θ——暖管蒸汽溫度與暖管前鋼管溫度差，℃
根據完全彈性碰撞的能量守恒定律[3]，得：
 
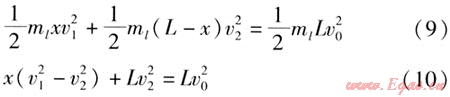
由(6)、(8)、(10)得：
 
由此可得暖管過程中管段AC最大動能的計算式為：
 
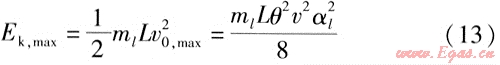
式中Ek,max——暖管過程中管段AC的最大動能，J
根據能量守恒定律，暖管過程中，管段AC由最大動能Ek,max到動能消失為靜止，能量由固定支座B的彈性形變、兩端波紋管補償器的彈性形變、滑動支架的摩擦消耗。可寫出能量平衡式：
 
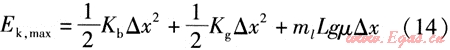
式中Kb——波紋管補償器的彈性系數，N/m
    △x——暖管時固定支座B的最大振幅，m
    Kg——固定支座的彈性系數，N/m
    g——重力加速度，m/s2
    μ——滑動支架的摩擦系數
聯立式(13)、(14)，得到采用波紋管補償器時，暖管過程中固定支座B最大振幅的計算式：
 
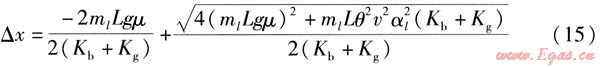
一般情況下，與管道對固定支座的沖擊力相比，波紋管補償器彈性力、滑動支架摩擦力較小。若忽略波紋管補償器彈性力、滑動支架摩擦力，暖管時固定支座的最大振幅為：
 
    暖管時管道對固定支座B的最大沖擊力為：
    Fmax=Kg△x    (17)
式中Fmax——暖管時管道對固定支座的最大沖擊力，N
將式(16)代入式(17)得：
 
    由于在式(18)的推導過程中，忽略了暖管時管壁的傳熱過程、波紋管補償器彈性力、滑動支架摩擦力，因此式(18)是分析暖管時管道對固定支座最大沖擊力的近似計算式。由式(18)可知，在蒸汽管道暖管時，管道對固定支座的最大沖擊力與暖管蒸汽溫度、流速的變化規律基本一致。因此，CJJ 28—2004《城鎮供熱管網工程施工及驗收規范》要求暖管速度不宜過快是有道理的。
3 彈性固定支座設計理論
    在目前的蒸汽管道設計中，部分人不考慮暖管動能對固定支座產生的沖擊以及引起固定支座變形或振動問題。若出現暖管振動造成固定支座破壞，大多把問題簡單歸結為暖管蒸汽流速過高。然而在理論上，若固定支座為絕對剛性(即Kg無窮大)，由式(18)可知，暖管時管道對固定支座的最大沖擊力將趨近于無窮大，固定支座必然遭到破壞。當然，在現實中絕對剛性的固定支座不可能存在，因此按照有關規定緩慢暖管一般不會造成固定支座破壞。
    反之，Kg值越小，固定支座越富有彈性，暖管時管道對固定支座的沖擊力越小。在理論上，根據式(18)，可得出保證固定支座安全可靠的彈性系數計算式：
   
式中Ft——固定支座設計推力，N
    我國幾家生產鋼套鋼直埋蒸汽管道的廠家注意到了剛性固定支座易遭到破壞的問題，設計生產了鋼套鋼彈性內固定支座，在工程實踐中廣泛應用，效果很好。
4 結論
    由分析可知，固定支座間距越大，暖管時管道對固定支座的沖擊力越大。受到套筒補償器、波紋管補償器、方形補償器等常用補償器補償量的限制，固定支座間距一般較小。隨著旋轉補償器的出現，單組旋轉補償器的補償段長度可達到200m或更長。因此，對于補償器補償段長度較長的供熱管道工程，固定支座的設計以及暖管蒸汽溫度、流速的設定，更應該考慮暖管時管道對固定支座的沖擊。
參考文獻：
[1] CJJ 28—2004，城鎮供熱管網工程施工及驗收規范[S].
[2] CJJ 104—2005，城鎮供熱直埋蒸汽管道技術規程[S].
[3] 董云峰，段文峰.理論力學[M].北京：清華大學出版社.2006.
 
(本文作者：王玉玄1，2 高百爭2 劉德平1 1.鄭州大學機械工程學院 河南鄭州 450001；2.鄭州市熱力總公司 河南鄭州 450052)