摘要：論述了適用于居民生活用氣量指標的數理統計學模型和計量經濟學模型的理論基礎、樣本構成、建模過程以及各自的優點及存在的問題，提出應將數理統計學模型與計量經濟學模型相結合，進行居民生活用氣量指標的現狀值評估、彈性分析、未來發展趨勢預測。
關鍵詞：居民生活用氣量指標；數理統計學模型；計量經濟學模型；現狀值評估；彈性分析；趨勢預測；影響因素
1 概述
進入21世紀以來，隨著天然氣資源的開發，長輸管道工程的全面啟動和城市天然氣利用工程項目大范圍建設，天然氣作為優質、高效的一次能源將在我國居民生活能源中占據重要地位[1]。居民生活用氣量指標，即每位居民每年消耗燃氣的折算熱量，是反映居民生活燃氣消耗水平的一個綜合指標。該指標的現狀及其發展趨勢是簽訂燃氣供氣合同、建設燃氣輸配系統的重要基礎數據。對居民生活用氣量指標影響因素的彈性分析，可以為決策者制定更為合理的民用天然氣政策提供依據。
居民生活用氣量指標的研究始于20世紀60年代，由于受到居民用戶數量多、影響因素復雜、重視程度不足等條件制約，關于這方面的研究較少。目前有兩種理論用于居民生活用氣量指標的研究：①基于數理統計學理論建立的模型，即數理統計學模型。在該模型中居民生活用氣數據被視為隨機變量，通過隨機抽取的居民生活用氣數據子樣，證明居民生活用氣數據總體服從正態分布，進而運用數理統計定理，得到在一定置信度下的居民生活用氣量指標現狀值的置信區間。②基于計量經濟學理論建立的模型，即計量經濟學模型。在該模型中居民生活用氣量指標與其影響因素之間存在量化關系，通過該模型可以進行居民生活用氣量指標的彈性分析及未來發展趨勢的預測。
本文對居民生活用氣量指標的兩種模型進行分析。從兩種模型的理論基礎、樣本構成、建模過程等角度分別進行闡述，在綜合分析了兩種模型各自的優點及存在的問題的基礎上，提出應將數理統計學模型與計量經濟學模型相結合，進行居民生活用氣量指標現狀值評估、彈性分析、未來發展趨勢預測。
2 數理統計學模型
數理統計學是研究隨機現象的統計規律的數學學科[2]?；诰用裆钊細庀牡碾S機特性，我們可以采用數理統計學模型研究居民生活用氣量指標[3、4]。
在居民生活用氣量指標數理統計學模型中，隨機抽取n個居民生活年燃氣消耗量數據(單位為m3/(人·a))，作為樣本。
居民生活年燃氣消耗量是隨機變量，居民生活年燃氣消耗量的數據全體為總體，記為ζ，各個居民生活年燃氣消耗量的數據為個體，記為ζi，n個個體ζi組成總體的一個子樣，計為ζ。
ζ={ζ1，ζ2，…，ζn) (1)
根據統計量定義，子樣ζ的子樣均值和子樣方差分別為式(2)、(3)：
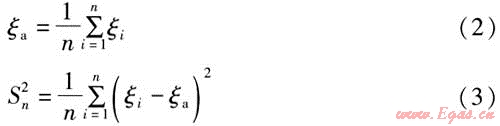
式中ζa——子樣均值，m3/(人·a)
n——子樣中隨機變量的數量
i——子樣中隨機變量的序號
ζi——第i個個體，m3/(人·a)
Sn2——子樣方差，[m3/(人·a)]2。
文獻[3]進行了居民生活年燃氣消耗量的隨機分析，根據隨機抽取的居民生活年燃氣消耗量子樣，證明居民生活年燃氣消耗量的數據總體f服從正態分布，即
ζ～N(μ，σ2) (4)
式中ζ——居民生活年燃氣消耗量的數據總體
μ——總體均值，m3/(人·a)
σ2——總體方差，[m3/(人·a)]2
總體均值μ即為居民生活用氣量指標，通過對總體均值μ進行區間估計，即可得到在一定置信度下的居民生活用氣量指標現狀值的置信區間。
根據數理統計定理，取自正態總體的子樣ζ，其子樣均值ζa、子樣方差Sn2、總體均值μ、總體標準差Sn構成統計量A，A是自由度為n-1的t變量，它服從t(n-1)分布。
在t分布表中，查出顯著性水平α、自由度n-1對應的臨界值t(α)(n-1)，使得：
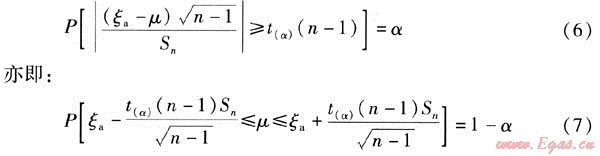
式中α——顯著性水平
t(α)(n-1)——t分布表中顯著性水平α、自由度n-1對應的臨界值
置信度為1-α的居民生活用氣量指標總體均值μ的置信區間為：
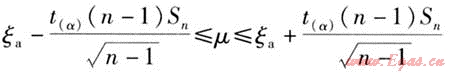
居民生活用氣量指標數理統計學模型樣本構成簡單，建模求解過程簡便，對現狀值的區間估計準確。但它無法研究各種因素對居民生活用氣量指標的影響，對未來發展趨勢不能作出預測。
3 計量經濟學模型
計量經濟學是經濟學、統計學、數學綜合形成的邊緣學科，是以揭示經濟活動中客觀存在的數量關系為內容的經濟學學科[5]。將計量經濟學應用于居民生活用氣量指標的研究[6、7]，是借鑒國外電力領域中將計量經濟學應用于居民生活用電需求研究的成果[8～11]，并基于居民生活燃氣需求與用電需求的相似性而發展起來的。
居民生活用氣量指標的計量經濟學模型，根據采集的數據樣本的不同可以分為橫截面模型、時間序列模型、面板數據模型。橫截面模型是對一個或多個變量在同一時間點上收集的數據進行建模，時間序列模型是對同一個變量在不同時間點上的數據進行建模，面板數據模型是對一個或多個變量在不同時間點上的數據進行建模。由于我國城市燃氣發展歷史較短，居民生活燃氣消耗數據積累較少，采用橫截面模型進行居民生活用氣量指標研究的條件較為成熟。
居民生活用氣量指標橫截面模型采集樣本過程比數理統計學模型復雜。需要隨機抽取n戶居民一年的燃氣消耗量及與燃氣使用相關的基本信息，包括：燃氣價格、戶年收入、戶人口數、燃氣設備擁有情況、燃氣使用習慣、能替代燃氣的其他家用能源價格等項目(針對不同居民總體的生活燃氣消耗特點而有所不同)。
根據微觀計量經濟學需求模型[12]，居民生活燃氣需求函數可以表示為：
q=f(P，I，D，M，N，V) (8)
式中q——居民生活年燃氣消耗量，J/(人·a)
P——燃氣價格，元/J
I—一用戶年收入，元/(戶·a)
D——用戶人口數，人/戶
M——用戶燃氣設備擁有情況
N——用戶燃氣使用習慣
V——能替代燃氣的其他家用能源價格，元/J
在橫截面模型研究時，常遇到異方差問題。根據相關文獻，半對數計量經濟學需求模型在減少異方差以及極端值影響方面有著獨特的優越性[13]。因此，居民生活用氣量指標研究推薦采用半對數計量經濟學需求模型，即：
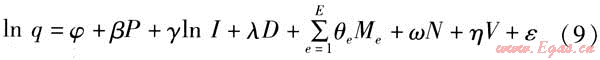
式中Me——用戶擁有第e種燃氣設備的情況
E——用戶擁有燃氣設備的總數，臺
φ、β、γ、λ、θe、ω、η——回歸參數
ε——不確定因素的影響，即隨機干擾項
其中，P、I、D、V反映連續變量對居民生活燃氣消耗量的影響，為實際數值；Me、N是為反映定性變量對居民生活燃氣消耗量的影響而虛構的數值，稱為虛擬變量(例如：擁有第e種燃氣設備，則Me=1，否則Me=0；用戶燃氣使用習慣為寬松型，則N=1，否則N=0)。
根據橫截面數據樣本，采用最小二乘法對式(9)進行參數估計，得到滿足經典回歸假設檢驗的回歸參數。求解回歸參數估計量程序流程見圖1。
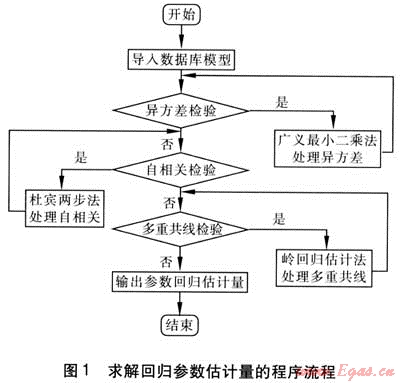
對求得的回歸參數進行t檢驗，若回歸參數的t統計量滿足式(10)，則認為此回歸參數對應的項目對居民生活年燃氣消耗量q有顯著影響，否則認為影響不顯著。
根據式(9)對居民生活用氣量指標進行彈性分析。彈性分析的目的在于得到居民生活用氣量指標對其影響因素的微小變化所做出的反應。居民生活用氣量指標相對各項影響因素的彈性如下：
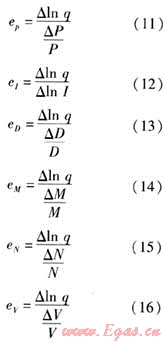
式中ep——居民生活用氣量指標對燃氣自身價格的彈性
eI——居民生活用氣量指標對用戶年收入的彈件
eD——居民生活用氣量指標對用戶人口數的彈性
eM——居民生活用氣量指標對燃氣設備數量的彈性
eN——居民生活用氣量指標對燃氣使用習慣的彈性
eV——居民生活用氣量指標對能替代燃氣的其他家用能源價格的彈性
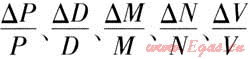——各項影響因素的變動率 以上居民生活用氣量指標的彈性分析數據，可以為決策者制定民用天然氣政策提供參考，以利于節約用氣、合理用氣。
依據式(9)及居民生活用氣量指標的彈性分析數據，再參照社會、經濟等發展趨勢預測報告，預測未來居民生活用氣量指標影響因素的發展變化，即可得到居民生活用氣量指標的未來發展趨勢。隨著我國民用天然氣事業的發展和居民生活用氣數據的積累，采集時間序列數據和面板數據構建居民生活用氣量指標時間序列和面板數據計量經濟學模型，將是居民生活用氣量指標計量經濟學模型研究的未來發展方向，它將使居民生活用氣量指標的未來發展趨勢預測具有更為可靠的精度。
計量經濟學模型建立了居民生活用氣量指標與其影響因素之間的量化模型。其意義在于，從量的角度說明了居民生活用氣量指標與其影響因素之間的關系?？梢酝ㄟ^影響因素的發展趨勢，預測居民生活用氣量指標的未來發展趨勢；也可以通過政策調控影響因素，使居民生活用氣量指標向著預定的方向發展。
4 結論
① 對于居民生活用氣量指標的兩種模型，數理統計學模型具有樣本構成簡單、建模求解過程簡便、現狀值區間估計準確等優點，適用于現狀值的評估。計量經濟學模型構建了居民生活用氣量指標與其影響因素間的量化模型，適用于彈性分析以及未來發展趨勢的預測。
② 居民生活用氣量指標作為反映居民生活燃氣消耗水平的一個綜合指標，用于指導燃氣規劃及工程建設，它的現狀值評估和未來發展趨勢預測密不可分。對于這一指標的深刻剖析，可以為制定合理的民用天然氣政策提供依據。對比分析兩種模型自身的特點，本文推薦應將數理統計學模型與計量經濟學模型相結合，進行居民生活用氣量指標現狀值評估、彈性分析、未來發展趨勢預測。
參考文獻：
[1] 劉增潔.世界天然氣市場回顧及未來展望[J].中國能源，2002，(7)：30-34.
[2] 魏宗舒.概率論與數理統計教程[J].北京：高等教育出版社，1983.
[3] 張蔚東，方育渝，李恩山.居民燃氣消耗量的隨機分析[J].煤氣與熱力，1989，9(1)：34-39.
[4] 盛凱橋，張亦軍，康志剛，等.武漢居民生活用氣定額及不均勻性分析[J].煤氣與熱力，2001，21(5)：20-21.
[5] 李寶仁.計量經濟學[M].北京：中國財政經濟出版社，2002.
[6] 馬迎秋.上海居民生活用氣指標的研究(碩士學位論文)[DL、哈爾濱：哈爾濱工業大學，2004.
[7] 焦文玲，吳念劬，馬迎秋，等.上海居民生活用氣量指標分析[J].天然氣工業，2008，28(1)：143-145.
[8] HAAS R，BIERMAYR P，ZOECHLING J，et al. Impacts on electricity consumption of household appliances in Austria：a comparison of time series and cross-section analysis[J].Energy Policy，1998，(26)：1031*1040.
[9] TIWARI P. Architectural，demographic，and economic causes of electricity consumption in Bombay[J].Journal of Policy Modeling，2000，(22)：81-98.
[10] SARAK H，SATMAN A. The degree-day method to estimate the residential heating natural gas consumption in Turkey：a case study[J].Energy，2003，(28)：929-939.
[11] BRANCH E R. Short run income elasticity of demand for residential electricity using consumer expenditure survey data[J].The Energy Journal，1993，(14)：111-121.
[12] 段進明.微觀經濟學[M].北京：中國政法大學出版社，2002.
[13] HSING Y. On the variable elasticity of the demand for gasoline[J].Energy Economics，1990，(12)：132-136.
(本文作者：馬迎秋 上海燃氣工程設計研究有限公司 上海 200070)
贊 賞 分享
您可以選擇一種方式贊助本站
支付寶轉賬贊助
微信轉賬贊助
- 注解：本資料由會員及群友提供僅供閱讀交流學習，不得用于商業用途！
