然氣的混合問(wèn)題,建立了氣水兩相滲流模型及氣體擴(kuò)散模型,建立了二維平面有限元模型,采用部分離散方法對(duì)數(shù)學(xué)模型進(jìn)行了有限元方程的推導(dǎo)。應(yīng)用建立的模型進(jìn)行含水層型地下儲(chǔ)氣庫(kù)以惰性氣體作為部分蟄層氣的建庫(kù)過(guò)程和工業(yè)運(yùn)行的數(shù)值模擬。通過(guò)對(duì)單井儲(chǔ)氣庫(kù)注采進(jìn)行數(shù)值模擬,分析了在注采過(guò)程中對(duì)采出氣質(zhì)量影響較大的參數(shù)。
關(guān)鍵詞:含水層型地下儲(chǔ)氣庫(kù);墊層氣;數(shù)值模擬;惰性氣體;采出氣質(zhì)量
Numerical Simulation of Using Inert Gas as Cushion Gas in Aquifer Underground Gas Storage Reservoir
LI peiming,LI Juanjuan
Abstract:The mixing between inert gas and natural gas is studied under the condition that inert gas substitutes natural gas as cushion gas in aquifer underground gas storage reservoir.A gas-water two phase flow model,a gas diffusion model and a two-dimensional plane strain finite element model are established.The finite element equation is deduced by the semi-discrete method.The construction process and industrial operation of aquifer underground gas storage reservoir using inert gas as partial cushion gas are simulated using the developed model.Through the numerical simulation of a single well injection and withdrawal,the factors influencing the withdrawn gas quality during the injection and withdrawal are analyzed.
Key words:aquifer underground gas storage reservoir;cushion gas;numerical simulation;inert gas;withdrawn gas quality
1 概述
含水層型地下儲(chǔ)氣庫(kù)是指為了達(dá)到儲(chǔ)氣目的,人為地用壓縮機(jī)加壓,通過(guò)氣井將天然氣注入到地下合適的含水層中,將含水層巖層孔隙中的水排走,在非滲透性的含水蓋層下直接形成的儲(chǔ)氣場(chǎng)所。含水層型地下儲(chǔ)氣庫(kù)在天然氣的開發(fā)和利用過(guò)程中起著舉足輕重的作用,如可以協(xié)調(diào)天然氣供求關(guān)系與調(diào)峰[1],保證供氣可靠性和連續(xù)性等。
在儲(chǔ)氣庫(kù)注采過(guò)程中,為抑制地層水流動(dòng),防止水侵入和保證儲(chǔ)氣庫(kù)工作的穩(wěn)定性,需要一定量的墊層氣。墊層氣量一般為儲(chǔ)氣庫(kù)儲(chǔ)氣量的30%~70%,平均占儲(chǔ)氣層體積的50%[2]。以廉價(jià)的惰性氣體代替天然氣作為墊層氣具有非常重要的經(jīng)濟(jì)意義,在國(guó)外已成功進(jìn)行了實(shí)踐。但是,在儲(chǔ)氣庫(kù)運(yùn)行過(guò)程中,惰性氣體與天然氣會(huì)發(fā)生混合擴(kuò)散,主要依靠分子擴(kuò)散和對(duì)流擴(kuò)散。分子擴(kuò)散是由于儲(chǔ)氣庫(kù)不同位置各氣體濃度不同而導(dǎo)致氣體由高濃度處流向低濃度處;對(duì)流擴(kuò)散是由于氣體在儲(chǔ)氣庫(kù)中的整體滲流流動(dòng)而引起的物質(zhì)傳遞。惰性氣體與天然氣混合的程度決定了采出氣中惰性氣體的含量,因此,在儲(chǔ)氣庫(kù)運(yùn)行過(guò)程中,確定儲(chǔ)氣庫(kù)內(nèi)氣體濃度分布情況及控制采出氣中惰性氣體的含量具有非常重要的意義[3]。
本文通過(guò)建立氣水兩相滲流模型及氣體擴(kuò)散模型,采用有限元求解方法,動(dòng)態(tài)確定儲(chǔ)氣庫(kù)壓力、含水飽和度及氣體濃度分布情況。同時(shí),通過(guò)對(duì)封閉邊界條件含水層型地下儲(chǔ)氣庫(kù)進(jìn)行數(shù)值模擬,對(duì)注采過(guò)程中影響采出氣質(zhì)量較大的參數(shù)進(jìn)行分析。
2 數(shù)學(xué)模型的建立[4]
2.1 氣水兩相滲流模型
本文的數(shù)學(xué)模型中,將氣水滲流視為等溫過(guò)程,假設(shè)氣水互不相溶,考慮毛管壓力的影響[5~6],不考慮巖石的壓縮性。
在地層中取一個(gè)微元六面體進(jìn)行分析,設(shè)氣水共同充滿孔隙空間,不考慮氣水兩相間的質(zhì)量轉(zhuǎn)移。根據(jù)質(zhì)量守恒原理,可得連續(xù)性方程:

以惰性氣體代替部分墊層氣時(shí),墊層氣與天然氣之間會(huì)發(fā)生相互摻混。由分子擴(kuò)散的斐克定律,對(duì)微元體進(jìn)行分析,可得氣體對(duì)流擴(kuò)散方程,見式(3),式(3)分別對(duì)應(yīng)天然氣與墊層氣2種氣體。
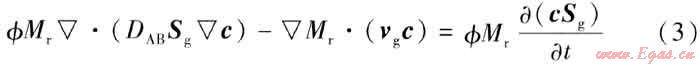
式中Mr——氣體的相對(duì)分子質(zhì)量
DAB——組分A在介質(zhì)B中的擴(kuò)散系數(shù)
c——氣體的濃度,kmol/m3
考慮氣水相流動(dòng)時(shí)分別服從達(dá)西滲流定律,則有運(yùn)動(dòng)方程:

對(duì)于氣相,必須滿足氣體狀態(tài)方程:
pgV=ZnRT (6)
式中V——氣體的體積,m3
Z——壓縮因子
n——氣體的物質(zhì)的量,mol
R——氣體常數(shù),J/(mol·K)
T——氣體溫度,K
飽和度平衡方程:
Sg+Sw=1 (7)
氣水兩相系統(tǒng)毛管壓力方程:
pc=pg-pw=f(Sw) (8)
式中pc——毛管壓力,Pa
f(Sw)——含水飽和度的函數(shù),Pa
將氣水滲流連續(xù)性方程、運(yùn)動(dòng)方程、氣體狀態(tài)方程、飽和度平衡方程以及毛管壓力方程整理后,得到氣水兩相滲流方程為:
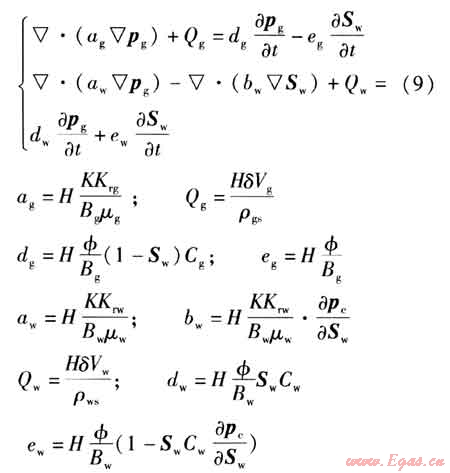
式中H——維數(shù)因子
K——儲(chǔ)層的絕對(duì)滲透率,md
Krg——氣相相對(duì)滲透率
Bg——氣體的地層體積系數(shù)
δ——常數(shù),在井點(diǎn)處δ=1,在非井點(diǎn)處δ=0
Vg——氣體產(chǎn)量,m3,注入井Vg取正值,采氣井Vg取負(fù)值
ρgs——氣體在標(biāo)準(zhǔn)狀態(tài)下的密度,kg/m3
Cg——氣體的等溫壓縮系數(shù)
Krw——水相相對(duì)滲透率
Bw——水的地層體積系數(shù)
Vw——水的產(chǎn)量,m3,注入井K取正值,采氣井K取負(fù)值
ρws——水在標(biāo)準(zhǔn)狀態(tài)下的密度,kg/m3
Cw——地層水的壓縮系數(shù)
2.2 氣體擴(kuò)散模型
以惰性氣體代替天然氣作為部分墊層氣時(shí),惰性氣體與天然氣之間會(huì)發(fā)生相互混合擴(kuò)散。建立的氣體擴(kuò)散連續(xù)性方程如下:
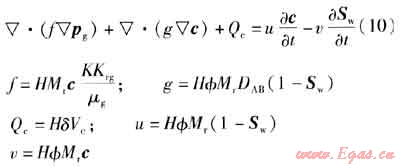
式中Vc——采出氣中組分氣體的體積,m3
2.3 邊界條件和初始條件
① 邊界條件
含水層型地下儲(chǔ)氣庫(kù)數(shù)值模擬中的邊界條件可分為外邊界條件和內(nèi)邊界條件兩大類。儲(chǔ)氣庫(kù)為外邊界條件,井點(diǎn)(因?yàn)闅饩霃脚c井距或儲(chǔ)氣庫(kù)范圍相比較小,所以可以把氣井作為點(diǎn)匯或點(diǎn)源處理,簡(jiǎn)稱井點(diǎn))為內(nèi)邊界條件。
② 初始條件
開始儲(chǔ)氣庫(kù)內(nèi)完全被水充滿,含水飽和度為1,初始?jí)毫榈貙悠骄鶋毫ΑN醋⑷肴魏螝怏w時(shí),氣體的初始濃度皆為0。當(dāng)向儲(chǔ)氣庫(kù)注入一定量的惰性氣體作墊層氣之后,下一階段開始時(shí)天然氣的初始濃度仍為0,而惰性氣體的初始濃度為注入結(jié)束時(shí)的濃度。
3 模型的求解
對(duì)于含水層型地下儲(chǔ)氣庫(kù),因?yàn)楹畬拥暮穸扰c其底面積相比較小,且一般性質(zhì)較均勻,垂向物性變化小,所以可采用二維模型進(jìn)行分析,以使問(wèn)題簡(jiǎn)化,且計(jì)算精度影響不大[6]。對(duì)于氣井,將氣井視為點(diǎn)源或點(diǎn)匯。
3.1 有限元方程推導(dǎo)
本文討論的是非穩(wěn)態(tài)的氣水滲流、氣氣擴(kuò)散問(wèn)題,各參數(shù)不僅是空間域的函數(shù),而且是時(shí)間域的函數(shù),因此建立有限元方程時(shí)采用部分離散的方法[7]。對(duì)空間域的離散采用Galerkin有限元方法,對(duì)時(shí)間域的離散采用有限差分法,把型函數(shù)僅表示成空間坐標(biāo)的函數(shù),而節(jié)點(diǎn)的函數(shù)值則是時(shí)間t的函數(shù)。G表示一個(gè)有界的可度量幾何形體,在此表示積分區(qū)域。當(dāng)G為平面有界閉區(qū)域時(shí),記為D;格林公式中,當(dāng)G為空間有限曲線段時(shí),記為Γ。
通過(guò)選取權(quán)函數(shù),得Galerkin法的基本表達(dá)式如下:
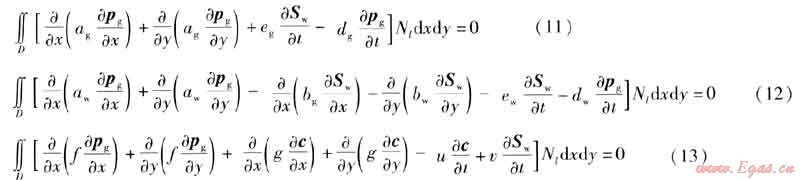
式中x、y——坐標(biāo)
Nl——型函數(shù)
Green公式為:
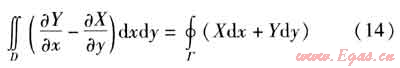
式中Y、X——被積函數(shù)
利用Green公式對(duì)式(11)~(13)進(jìn)行分部積分,并代入邊界條件,整理后得:

式中l(wèi)——節(jié)點(diǎn)編號(hào),l=1,2,…,n
n——節(jié)點(diǎn)個(gè)數(shù)
式(15)~(17)為二維氣水滲流及氣體擴(kuò)散有限單元法計(jì)算的基本方程。
3.2 有限元程序的實(shí)現(xiàn)
本文對(duì)有限元方程的求解利用Matlab語(yǔ)言進(jìn)行編程實(shí)現(xiàn)。有限元法程序按照功能可分為3個(gè)組成部分:前處理程序、有限元分析本體程序、后處理程序。前處理程序主要進(jìn)行網(wǎng)格剖分,并將得到的數(shù)據(jù)傳遞給本體程序。有限元分析本體程序主要完成各種參數(shù)計(jì)算,得到單元?jiǎng)偠染仃嚥卧獎(jiǎng)偠染仃嚭铣蔀榭傮w矩陣,對(duì)總體矩陣進(jìn)行求解[8]。參數(shù)計(jì)算、單元?jiǎng)偠染仃囉?jì)算由子程序完成,計(jì)算完成后傳遞給主程序。后處理程序可方便輸出所需要的各種數(shù)據(jù),并方便及時(shí)地提供圖形顯示,如壓力、飽和度、濃度分布圖等。
根據(jù)建立的數(shù)值模型,通過(guò)選取算例進(jìn)行求解,可模擬出儲(chǔ)氣庫(kù)建庫(kù)及動(dòng)態(tài)運(yùn)行過(guò)程中,儲(chǔ)氣庫(kù)內(nèi)各點(diǎn)壓力、含水飽和度、氣體濃度分布情況,模擬結(jié)果符合儲(chǔ)氣庫(kù)運(yùn)行動(dòng)態(tài)變化趨勢(shì)。
4 模擬算例
假設(shè)一理想的封閉邊界條件含水層型地下儲(chǔ)氣庫(kù),地層均質(zhì),厚度為5m。初始地層壓力為8.4MPa,地層溫度為21℃,絕對(duì)滲透率為270md,有效孔隙度為0.125。
本文討論單井注采氣情況,假定目標(biāo)注氣量為0.1×108m3,儲(chǔ)氣庫(kù)中心為注采井,注采速度為8.64×104m3/d。在儲(chǔ)氣庫(kù)邊界上設(shè)8口排水井,每口排水井的排水量為86.4m3/d,采氣時(shí),排水井均關(guān)閉。
建庫(kù)初期,先向儲(chǔ)氣庫(kù)中注入氮?dú)庾鳛椴糠謮|層氣,假設(shè)氮?dú)饽繕?biāo)注入量為1×106m3,注入到第12d時(shí),氮?dú)饬窟_(dá)到1036800m3,此時(shí)停止注入。
之后開始向儲(chǔ)氣庫(kù)注入天然氣,運(yùn)行到第116天時(shí),累積注入量(10022400m3)約達(dá)到目標(biāo)注氣量,停止注氣。天然氣注入結(jié)束時(shí),儲(chǔ)氣庫(kù)內(nèi)天然氣及氮?dú)獾捏w積分?jǐn)?shù)見圖1、2。由圖1、2可知,隨著天然氣的注入,天然氣逐漸將氮?dú)庀蛑車?qū)開,因而注采井周圍區(qū)域?yàn)榧兲烊粴鈪^(qū);由于氣體擴(kuò)散,天然氣與氮?dú)庀嗷交欤蚨鴱淖⒉删饾u向外,天然氣的體積分?jǐn)?shù)逐漸減小,氮?dú)獾捏w積分?jǐn)?shù)逐漸增大,形成天然氣與氮?dú)獾幕旌蠋В辉僦饾u向外,為純氮?dú)鈪^(qū)。

注氣結(jié)束后,關(guān)井穩(wěn)定20d,以使儲(chǔ)氣庫(kù)內(nèi)各點(diǎn)的壓力基本達(dá)到平衡狀態(tài),穩(wěn)定之后進(jìn)行回采。由于氣體相互擴(kuò)散,兩種氣體的混合帶逐漸變寬,隨著注采井壓力的下降,水會(huì)逐漸侵入。運(yùn)行到第184天時(shí),注采井的含水飽和度超過(guò)0.5,認(rèn)為對(duì)回采不利,此時(shí)停止采氣,儲(chǔ)氣庫(kù)內(nèi)天然氣及氮?dú)獾捏w積分?jǐn)?shù)見圖3、4。

截至停止采氣時(shí),儲(chǔ)氣庫(kù)剩余氣量為5875200m3,這部分氣體即為墊層氣,原儲(chǔ)氣庫(kù)的總氣量為10022400m3,則墊層氣量占總儲(chǔ)氣庫(kù)儲(chǔ)氣量的58.62%。而初始氮?dú)庾⑷肓繛?036800m3,則注入氮?dú)饬空級(jí)|層氣量的17.65%。
圖5、6為儲(chǔ)氣庫(kù)運(yùn)行過(guò)程中注采井天然氣及氮?dú)怏w積分?jǐn)?shù)變化情況。最初12d為注入氮?dú)怆A段,天然氣的濃度為0。第13天開始注入天然氣,由于氣體擴(kuò)散,注采井處的天然氣濃度會(huì)逐漸變大,井口處天然氣濃度上升很快。運(yùn)行到第22天時(shí),井口處天然氣體積分?jǐn)?shù)達(dá)到1,此后井口處一直為純天然氣。在回采過(guò)程中,初始時(shí)由于距注采井一定距離內(nèi)為純天然氣區(qū),采出氣中天然氣體積分?jǐn)?shù)仍為1。隨著采氣的進(jìn)行,天然氣與氮?dú)獾幕旌蠋Р粩嘞蜃⒉删幰苿?dòng),回采至第148天時(shí),開始出現(xiàn)氮?dú)猓藭r(shí)氮?dú)怏w積分?jǐn)?shù)為3×10-6。隨著回采的繼續(xù)進(jìn)行,采出氣中氮?dú)夂吭絹?lái)越大,到停止回采時(shí),氮?dú)怏w積分?jǐn)?shù)達(dá)9.665%。

5 采出氣質(zhì)量的影響因素分析
① 注入氮?dú)饬康挠绊?/span>
在初始建庫(kù)過(guò)程中,首先需要向儲(chǔ)氣庫(kù)中注入一定量的氮?dú)猓獨(dú)獾亩嗌賹?duì)采出氣中氮?dú)夂坑泻艽笥绊憽<俣▋?chǔ)氣庫(kù)總儲(chǔ)氣量仍為0.1×108m3,注采速度為8.64×104m3/d。要達(dá)到目標(biāo)注氣量,在注氣速度相同的情況下,需要注入116d。由于我們更關(guān)心采出氣的質(zhì)量,在此以回采到第165天為例,分析注入不同氮?dú)饬繒r(shí)采出氣的質(zhì)量,從而確定氣體的混合程度。
注入氮?dú)饬繉?duì)采出氣中天然氣和氮?dú)怏w積分?jǐn)?shù)的影響見圖7。由圖7可知,初始建庫(kù)時(shí)注入的氮?dú)饬吭蕉啵诤笃谧⒉商烊粴獾倪^(guò)程中,與天然氣混合的氮?dú)饬吭蕉啵瑥亩鴮?dǎo)致采出氣中氮?dú)饬吭蕉唷6趦?chǔ)氣庫(kù)建設(shè)時(shí),為了更大地節(jié)省投資費(fèi)用,氮?dú)獾淖⑷肓繎?yīng)該是越多越好。因此,必須確定合理的注入氮?dú)饬浚乖诓挥绊懖沙鰵赓|(zhì)量的情況下,注入更多的氮?dú)庖怨?jié)省投資費(fèi)用。

② 儲(chǔ)層絕對(duì)滲透率的影響
儲(chǔ)層絕對(duì)滲透率是影響注采效果的重要因素之一。假定儲(chǔ)氣庫(kù)總儲(chǔ)氣量為0.1×108m3,初始建庫(kù)時(shí)注入氮?dú)饬繛?×106m3,分析儲(chǔ)層絕對(duì)滲透率對(duì)儲(chǔ)氣庫(kù)注采過(guò)程的影響。
回采到第145天時(shí),儲(chǔ)層絕對(duì)滲透率對(duì)采出氣中天然氣體積分?jǐn)?shù)的影響見圖8。由圖8可知,回采相同時(shí)間時(shí),儲(chǔ)層絕對(duì)滲透率越大,采出氣中天然氣的體積分?jǐn)?shù)越小。因?yàn)閮?chǔ)層絕對(duì)滲透率越大,地層的水力傳導(dǎo)性越好,氮?dú)馀c天然氣的擴(kuò)散越容易,混合程度越大。

儲(chǔ)層絕對(duì)滲透率對(duì)墊層氣量占儲(chǔ)氣庫(kù)總氣量體積分?jǐn)?shù)的影響見圖9。以含水飽和度大于0.5為停止回采的條件,由圖9可知,儲(chǔ)層絕對(duì)滲透率越大,儲(chǔ)氣庫(kù)所需的墊層氣量越多。因此,從墊層氣量及氣體混合的角度分析,儲(chǔ)層絕對(duì)滲透率越小越好。但是在注氣過(guò)程中,絕對(duì)滲透率小的儲(chǔ)層,注氣井及地層平均壓力升高很快,對(duì)提高儲(chǔ)氣庫(kù)的總注氣量不利。因此,在實(shí)際工程中,應(yīng)綜合分析注采過(guò)程,選擇具有合適絕對(duì)滲透率的儲(chǔ)層,以使儲(chǔ)氣庫(kù)的運(yùn)行達(dá)到最優(yōu)化。

③ 儲(chǔ)層厚度的影響
由文獻(xiàn)[9]中的模擬可知,儲(chǔ)層越厚,地層平均壓力及井點(diǎn)壓力升高得越緩慢,因此,儲(chǔ)層越厚,對(duì)注氣量的提高越有利。然而,在相同注氣量及注采速度下,儲(chǔ)層越厚,注氣過(guò)程中,氣體驅(qū)開水的面積越小,那么在回采過(guò)程中,水會(huì)更快進(jìn)入注采井,使注采井含水飽和度更快達(dá)到0.5,此時(shí)應(yīng)停止采氣,則滯留在儲(chǔ)氣庫(kù)中的墊層氣量就越多(見圖10)。
回采到第145天時(shí),儲(chǔ)層厚度對(duì)采出氣中天然氣體積分?jǐn)?shù)的影響見圖11。由圖11可知,對(duì)于注入相同量的天然氣與氮?dú)猓瑑?chǔ)層厚度越大,兩種氣體混合的程度越大,從氣體混合角度分析,儲(chǔ)層厚度應(yīng)該越小越好,但儲(chǔ)層厚度越小,儲(chǔ)氣量越低。因此,應(yīng)當(dāng)綜合考慮多種因素,選取合適厚度的儲(chǔ)層。從圖11也可以看出,在儲(chǔ)層厚度為4~6m時(shí),采出氣中天然氣的體積分?jǐn)?shù)出現(xiàn)一個(gè)峰值,這就涉及到一個(gè)最佳儲(chǔ)層厚度的問(wèn)題,既要保證天然氣與氮?dú)獾幕旌铣潭炔挥绊懱烊粴獾氖褂茫忠WC儲(chǔ)氣庫(kù)的儲(chǔ)氣量。

④ 注采速度的影響
控制儲(chǔ)氣庫(kù)注采速度,確定最佳的注采速度,對(duì)儲(chǔ)氣庫(kù)的規(guī)劃設(shè)計(jì)十分重要。目前有些學(xué)者同時(shí)采用數(shù)值模擬和優(yōu)化分析的方法,來(lái)科學(xué)確定儲(chǔ)氣庫(kù)內(nèi)各單井的注采速度,獲得了較好的經(jīng)濟(jì)效益。
對(duì)于含水層型地下儲(chǔ)氣庫(kù),由于氣體黏度小于水的黏度,注氣速度過(guò)快易造成氣的突進(jìn),而注氣壓力和水層壓力之差不超過(guò)地層傾斜率就不容易將水排出。對(duì)于儲(chǔ)層較平的構(gòu)造,重力不起作用,注氣速度也不能太快,否則會(huì)造成氣體泄漏。對(duì)于不均質(zhì)的儲(chǔ)層,注氣時(shí)可注注停停,反復(fù)進(jìn)行多次,使氣體均勻推進(jìn)。同樣,采氣速度過(guò)快也會(huì)使壓降過(guò)大,邊、底水錐進(jìn)過(guò)快,則壓力漏斗所波及的范圍過(guò)大。一般為適應(yīng)高峰負(fù)荷,采氣速度可比注氣速度高4倍,正常情況下注氣、采氣速度均衡。
在目標(biāo)注氣量及注氣速度相同條件下,不同的采氣速度對(duì)儲(chǔ)氣庫(kù)運(yùn)行也有很大的影響(見圖12~15)。由圖12~15可知,采氣速度越快,地層平均壓力下降越快,注采井含水飽和度上升越快,天然氣與氮?dú)饣旌纤俣纫苍娇臁2蓺馑俣仍娇欤璧膲|層氣量越多,儲(chǔ)氣庫(kù)的回采率越低,而有時(shí)為了滿足調(diào)峰需要,可能需要較大的采氣速度。因此,必須綜合考慮各種因素,確定合理的采氣速度,保證調(diào)峰及采出氣體的質(zhì)量。


6 結(jié)論
本文建立了含水層型地下儲(chǔ)氣庫(kù)以惰性氣體作為墊層氣時(shí)氣水滲流、氣體擴(kuò)散的非穩(wěn)態(tài)數(shù)學(xué)模型,采用部分離散方法對(duì)方程進(jìn)行處理,對(duì)空間域利用Galerkin有限元方法進(jìn)行離散,對(duì)時(shí)間域利用有限差分方法進(jìn)行離散,利用Matlab語(yǔ)言對(duì)所建立的模型進(jìn)行編程求解,并利用所建立的模型選取算例進(jìn)行模擬。模擬研究結(jié)果對(duì)以惰性氣體作部分墊層氣的含水層型地下儲(chǔ)氣庫(kù)的建造及運(yùn)行具有一定理論指導(dǎo)意義和實(shí)用價(jià)值。
通過(guò)對(duì)含水層型地下儲(chǔ)氣庫(kù)以惰性氣體(氮?dú)?作為部分墊層氣模擬過(guò)程中的參數(shù)進(jìn)行分析,發(fā)現(xiàn)影響天然氣與氮?dú)鈣昆合的幾個(gè)重要參數(shù):建庫(kù)初始的注入氮?dú)饬亢艽蟪潭壬嫌绊懼烊粴馀c氮?dú)獾幕旌铣潭龋瑑?chǔ)層厚度、儲(chǔ)層絕對(duì)滲透率和采氣速度等都不同程度地影響著儲(chǔ)氣庫(kù)注采運(yùn)行的效果。在確定這些參數(shù)時(shí),并不是只要滿足氣體混合程度最低即可,因?yàn)樗鼈冞€制約著儲(chǔ)氣庫(kù)儲(chǔ)氣量、儲(chǔ)氣庫(kù)壓力變化、所需墊層氣量等其他參數(shù)。因此,在建設(shè)及運(yùn)行儲(chǔ)氣庫(kù)時(shí),應(yīng)當(dāng)綜合考慮經(jīng)濟(jì)因素以及各種降低氣體混合的措施等,確定合適的參數(shù)值,以使儲(chǔ)氣庫(kù)的運(yùn)行達(dá)到最優(yōu)化。
參考文獻(xiàn):
[1] 譚羽非,陳家新,嚴(yán)銘卿,等.天然氣地下儲(chǔ)氣庫(kù)季節(jié)性最大調(diào)峰量的確定[J].煤氣與熱力,2000,20(5):331-333.
[2] CARRIERE J F,F(xiàn)ASANINO G,TEK M R.Mixing in underground storage reservoirs[C]∥Proceedings of the 60th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers.Richardson(USA):Society of Petroleum Engineers,1985:1-12.
[3] 羅東曉,趙勤.地下儲(chǔ)氣庫(kù)技術(shù)的應(yīng)用與展望[J].煤氣與熱力,2008,28(7):B01-B03.

(本文作者:李佩銘1 李娟娟2 1.深圳市燃?xì)饧瘓F(tuán)股份有限公司 廣東深圳 518000;2.遼河油田鉆采工藝研究院 遼寧盤錦 124010)
贊 賞 分享
您可以選擇一種方式贊助本站

支付寶轉(zhuǎn)賬贊助

微信轉(zhuǎn)賬贊助
- 注解:本資料由會(huì)員及群友提供僅供閱讀交流學(xué)習(xí),不得用于商業(yè)用途!
網(wǎng)站VIP會(huì)員無(wú)限制下載網(wǎng)站資料!贊助網(wǎng)站獲得,點(diǎn)擊贊助!!
