摘要：壓縮機組振源較多，振動信號背景噪聲強烈、干擾大，通過檢測振動信號細微特征變化識別故障征兆異常困難。為此，從系統特性的角度出發，選擇信息熵及分形維數作為特征參數，提取氣閥無故障、輕微漏氣與嚴重漏氣3種典型故障信號特征，采用聚類分析方法來判斷氣閥故障。應用表明，較之傳統的診斷方法，基于譜熵及分形理論的診斷方法具有故障特征提取工作量小、容錯性強、準確率高的特點。

關鍵詞：壓縮機；氣閥；故障分析；高頻譜熵；分形維數

    壓縮機是天然氣工業中的關鍵設備，其工作狀態的好壞對于整個天然氣的生產、輸送起著至關重要的作用。壓縮機的故障診斷，一般采用時域特征值分析和頻譜分析的方法，從振動信號中提取故障分量^[1～3]。而在實際操作中，機組工況復雜，振源較多，干擾極大，理論計算得到的故障特征頻率往往與實測信號經一般頻譜分析后得到的響應信息缺乏一一對應的關系，因此僅僅通過檢測信號局部細微特征識別故障征兆往往并不準確。

    壓縮機組是一個復雜的耗散系統，對其進行診斷時，若能從整個系統行為的角度出發，分析其非線性特征，考查系統狀態演化的過程，則可以對整個壓縮機系統的行為有更深刻的了解。在系統論中，采用信息熵描述系統的有序程度，通過計算信息熵值揭示系統的狀態變化過程^[4～5]；在系統行為學中，利用分形理論揭示非線性運動行為本質特征，判斷機械設備系統的動力學特性改變^[6]。為此筆者根據信息熵原理，通過構造高頻譜熵描述氣閥信號的總體統計特性，將高頻譜熵及分形維數作為特征參數，提取了氣閥無故障、輕微漏氣與嚴重漏氣3種典型故障信號特征，最后采用聚類分析判斷氣閥故障。

    信息熵描述信號的總體統計特性，是衡量整個信號源在總體上的平均不確定性的量度^[7]。研究文獻表明，氣閥故障特征往往存在于信號的高頻段中^[8～9]，因此筆者定義高頻譜熵用于描述信號高頻段的統計特性，以提取氣閥信號特征。高頻譜熵利用功率譜高頻成分計算得到，具體構造如下。

設S_i為信號由時域變換到頻域所對應的功率譜，那么S={S₁，S₂，…，S_N)可看作是對原始信號的一種劃分，選定{S_N/2，S_N/2+1，…，S_N)作為高頻成分，根據文獻[5]對信息熵的解釋，定義高頻譜熵H_F為：

    因此，在氣閥的故障診斷中，可利用高頻譜熵對信號高頻段能量分布特性的概括能力，通過信號能量概率分布的均勻性來反映氣閥所處的狀態。氣閥正常信號能量是隨機分布的，系統無序，它所攜帶信息的不確定度大，熵值就高；異常信號中增加了確定性故障成分，且這種成分隨故障程度的增加而增加，系統變得有序，熵值便降低。

    分形是指事物表面上看起來雜亂無章，但存在自相似結構的一種現象，其基本參數是分形維數。對分形維數的定義大多基于“變尺度δ-覆蓋”的思想，即每次測量均忽略尺度小于δ時集合的不規則性，但考察δ→0時測量值的變化情況^[6]。

    分形維數有Hausdaorff維數、相似維數、容量維數、信息維數、關聯維數等幾種形式^[10]，在機械設備故障診斷中一般是計算信號的關聯維數。若分形集合中某2點之間的距離為ε，其關聯函數為C(ε)，則關聯維數為：

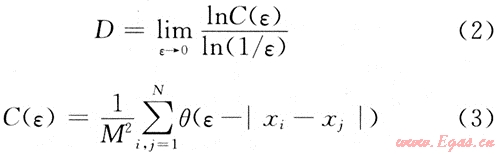
式中：M為相空間的相點數，θ為Heaviside函數。

    信號的分形維數越大，信號的局部起伏越大，信號相鄰點之間的相關性越弱，意味著信號頻譜結構中高頻成分較多；分形維數越小，信號的波動小，信號的相鄰點之間的相關性強，相應的，信號的高頻成分^[11]。

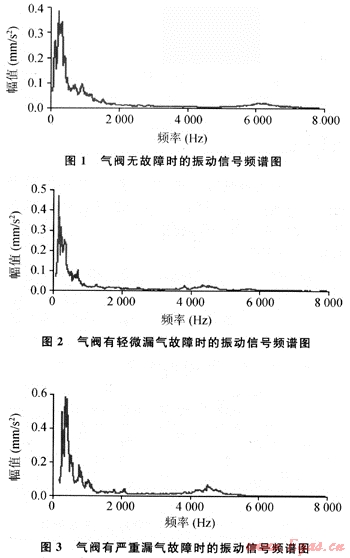
    應用上述理論方法對壓縮機氣閥典型故障下振動信號進行分析，試驗數據來源于塔里木油田某壓縮機，采集氣閥各典型故障下振動信號，采樣頻率F_S=16000Hz，數據長度N=61440，分別采集典型故障信號各5組，每組10個樣本。圖1～3分別為采集到的氣閥無故障、輕微漏氣、嚴重漏氣故障下的信號頻譜圖(因數據較多，僅列出每種典型故障下的1個振動信號樣本的頻譜圖)。

    計算各信號樣本的高頻譜熵和分形維數，表1僅列出了每組樣本的高頻譜熵和分形維數平均值。

故障模式	樣本號	高頻譜熵	分形維數
無故障	1	2.5630	1.2489
	2	2.5419	1.3528
	3	2.5601	1.2875
	4	2.5813	1.4019
	5	2.5672	1.2147
輕微漏氣	1	2.5410	1.6582
	2	2.5289	1.5732
	3	2.5236	1.4717
	4	2.5470	1.5691
	5	2.5306	1.5342
嚴重漏氣	1	2.4490	1.7676
	2	2.5012	1.7063
	3	2.4761	1.6938
	4	2.4379	1.7492
	5	2.4048	1.7615

從表1中可以明顯看出，隨著氣閥狀態的劣化，高頻譜熵值越來越小。根據信息熵理論，熵值越小，系統越有序，即信號中存在著某種謝定性成分，這與氣閥故障特征存在于信號高頻成分中，且隨著故障程度的增加而更加明顯這一事實完全符合(從頻譜圖1～3的高頻成分中可以明顯觀測到氣閥故障特征變化)；分形維數隨故障程度的增加呈遞增趨勢，分形維數越大說明信號的局部起伏越大，信號相鄰點之間的相關性越弱，意味著信號頻譜結構中高頻成分較多，而這正是氣閥存在故障的特征表現，結論與經典的頻譜分析完全吻合。

    表2列出了2個待檢信號的高頻譜熵及分形維數，采用聚類分析通過計算待檢狀態與各典型故障的歐氏距離判斷氣閥故障類型。取表1中的5個樣本平均值作為典型故障狀態特征值，對各參數[0，1]歸一化處理后計算其歐氏距離，列于表3。

特征值	無故障	輕微漏氣	嚴重漏氣	待檢狀態1	待檢狀態2
高頻譜熵	2.5627	2.5342	2.4538	2.5475	2.5013
分形維數	1.3012	1.5613	1.7357	1.4373	1.6082

狀態	L1	L2	L3
待檢狀態1	0.3429	0.3104	1.1009
待檢狀態2	0.9040	0.3208	0.5257

注：L₁、L₂、L₃分別表示待檢狀態與無故障、輕微漏氣、嚴重漏氣3種狀態的歐氏距離。

    對比表3中待檢狀態與各典型故障的歐氏距離，可以判斷2種待檢狀態均存在輕微漏氣故障，事后維修證實了該分析結果。

    針對壓縮機組振源多，信號背景噪聲強烈，干擾大的特點，提出將高頻譜熵及分形維數作為特征參數，考查氣閥無故障、輕微漏氣與嚴重漏氣3種典型故障振動信號的系統特性差異，采用聚類分析診斷氣閥故障。應用表明，該方法與傳統的時域特征值和頻譜分析相比具有明顯的優勢：不需檢測信號細微特征，極大地減小了故障特征提取的工作量；從整體系統特性考查信號故障特征，具有很強的容錯性，提高了診斷的準確率。

[1] 程香平，丁雪興，劉海亮，等.多種故障診斷技術在往復壓縮機中的應用[J].壓縮機技術，2007(5)：13-16.

[2] 張瓊，賀世正.改進BP網絡在離心式壓縮機故障診斷中的應用[J].現代機械，2007(5)：18-19.

[3] 馬波，高金吉，馮坤.能量算子在往復壓縮機故障診斷中的應用研究[J].機械科學與技術，2007，26(6)：696-700.

[4] 劉長虹，陳虬.基于信息熵理論中的含模糊參數的響應面法[J].機械強度，2003，25(2)：187-189.

[5] 申弢，黃樹紅，韓守木，等.旋轉機械振動信號的信息熵特征[J].機械工程學報，2001，37(6)：94-98.

[6] 王朝暉，張來斌.分形法在發動機隱含故障診斷中的應用[J].石油大學學報：自然科學版，2003，27(1)：54-57.

[7] 張新鋒，趙彥，施滸立.基于信息熵的結構廣義可靠度與模糊安全系數[J].中國機械工程，2007，18(14)：1735-1742.

[8] 王朝暉，姚德群，段禮祥.基于模糊聚類的油田往復壓縮機氣閥故障診斷研究[J].機械強度，2007，29(3)：521-524.

[9] 王成棟，朱永生，張優云，等.時頻分析與支持向量機在柴油機氣閥故障診斷中的應用[J].內燃機學報，2004，22(3)：245-251.

[10] 鄭洲順，曲選輝.PIM粉塵顆粒的分形特征及其分形維數[J].中國機械工程，2003，14(5)：436-439.

[11] 田立柱.基于混沌理論的機械設備故障診斷方法和技術研究[D].北京：石油大學(北京)，2003.

 

(本文作者：崔厚璽¹ 張來斌¹ 段禮祥¹ 秦才會² 1.中國石油大學(北京)機電工程學院；2.中海油服技術中心機電研究所)