摘要:酸氣回注是一種替代硫磺回收的經濟可行的酸氣處理方法,同時也是一種減少溫室氣體排放的環保方法。要確保正確地設計、實施和操作酸氣回注系統,首先就需要知道從井口到井底的回注流動情況、參數及相態分布,以確定酸氣回注系統所需的井口壓力。為此,建立了酸氣回注井筒多相流動通用模型。該模型描述了酸氣沿井筒的流動、參數及相態分布,其優點是能精確實現酸氣的性質和相平衡計算并綜合考慮酸氣井筒流動的質量、動量與能量守恒關系。所列舉的9個實際應用案例分析展示了新模型具有良好的應用效果。
關鍵詞:酸氣;H2S;CO2;回注;井筒;管道;多相流;相態
0 前言
隨著人們環境保護意識的日益增強,少量酸氣的處置就成了一個問題,生產商已不能像過去那樣將這些酸氣放空了,而將這些酸氣壓縮并注入不生產的地層就成為一種可選擇的替代方法。最近,人們又開始研究讓壓縮酸氣作為部分氣驅采油的利用價值,同時,酸氣回注也是一種減少溫室氣體排放的環保方法,這在《京都議定書》實施后顯得特別有意義。
井口到井底的流動和相態分布是酸氣回注系統設計及運行的關鍵參數,井口回注壓力估計的正確與否,對整個酸氣回注系統具有重要影響[1]。
精確模擬回注井筒流動和相態分布的困難在于井筒中酸氣熱力學性質的描述,即怎樣將井筒流體模型與其流動模型很好地結合起來,以形成一個完善的井筒回注流動模型。
筆者建立了酸氣回注井筒多相流動通用模型,該模型描述了酸氣沿井筒的流動、參數及相態分布。該模型的優點是綜合考慮了酸氣井筒流動的質量、動量與能量守恒關系,能精確實現酸氣的性質和相平衡計算。
1 基本模型
流體在井筒中的流動由其質量、動量與能量守恒定律來決定:

這3個質量、動量和能量守恒基本關系描述了井筒和管道內流體流動最一般的規律,對流動形式(穩態和瞬變流)、流體(氣體、液體和多相流體)以及流動方向和管道走向都沒有限制。該模型也考慮了管道和流體的壓縮性、流體與周圍環境的熱傳遞以及壓力和溫度對流體性質的影響。
作為管中流動的介質,流體的熱力學性質對流動模型有重大影響[2]。沿著井筒,由于流動、流體的重量和流體與地層的熱交換,流體的溫度和壓力都在不斷變化。因此流體的性質甚至相態都在不斷改變,一個適用于不同相態和流動條件(溫度、壓力)的流體模型是非常必要的。
在設計階段,通常會考慮井筒的穩定流動模型,這可通過將關系式中所有對時間的偏微分項設置為零來得到。
模型并未限制流動方向和管段走向,所以它可以用來描述垂直、水平和傾斜管段以及生產或回注井筒。
2 酸氣性質和井筒流動模型
由于溫度、壓力甚至相態的變化,沿井筒酸氣的性質會有很大的變化。在求解模型時,大量的計算用于估計流體的性質,一個精心設計的流體相平衡分析模型才能正確估計流體的特性。有很多流體相平衡分析模型,這里選用AQUAlibrium[3~4]來進行酸氣相平衡分析和性質計算,該模型具有較大的溫度和壓力范圍。
AQUAlibirum專為各種含水酸性天然氣的相平衡分析而設計,適用于酸性天然氣的氣、液和超臨界狀態。這一點很重要,因為回注酸氣往往在井口處于液相,而在井底處于超臨界狀態。此外,該模型是一個嚴格的熱力學模型,而非經驗模型。AQUAlibrium的另一個優點是它能平滑處理流體從液態或氣態到超臨界狀態的過渡,而很多流體性質計算軟件不能連續展示流體自液態到超臨界狀態的性質。這個連續性對正確理解酸氣回注系統的性質和求解井筒流動模型都很重要。
除了保證計算精度外,AQUAlibrium對井筒流動模擬還有以下幫助:
1) 它是油、氣、水三相模型,而酸性天然氣中常見的12個組分中也包含水。
2) 提供了油、氣、水各相的摩爾濃度及各相的8個性質,涵蓋井筒流動熱力學分析所需的所有性質。
3) 有足夠大的壓力和溫度范圍(150MPa和-150~300℃),對模型的迭代求解過程至關重要。
4) 所計算的焓包含相變過程所釋放的熱,使能量守恒關系描述得更精確。
對于給定的溫度和壓力,AQUAlibrium計算油、氣、水各相的摩爾濃度和性質、多相混合物的相關性質就可以由式(2)計算:
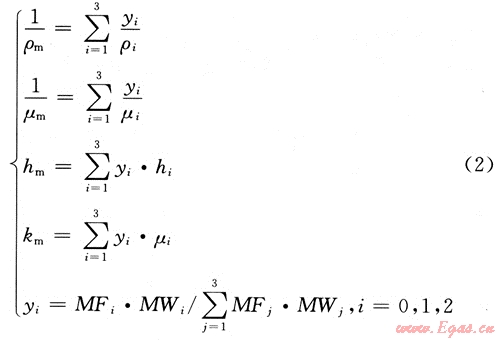
這些流體性質計算關系式適用于氣體(y0=1.0)、液體(y0=0.0)和多相流(0.0<y0<1.0)。下標i,j指流體的相態,其中氣相為0,水相為1,凝析相(非水相液體)為2。
由此,可得到下列井筒各種酸性天然氣多相流動模型,其流動方向不受限制[4]。
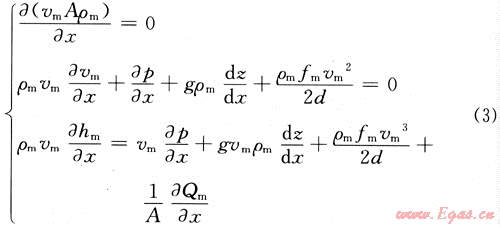
式中:壓力(p)、溫度(T)和混合流體的質量流量(Wm)是基本變量。混合流體的性質由AQUAlibrium根據流體的組分和流動條件來確定。多相流速砂。由式(4)計算:

井筒流動的摩阻系數由Colebrook-White關系式確定。
3 熱交換分析
井筒流體的溫度隨其所處的位置不同而顯著不同,有時還隨時間變化。很多流體的性質受溫度的影響,從而影響其水力學流動特征,如密度、黏度、甚至相態的變化,因此井筒流體和周圍環境的熱交換應該被包含在精確井筒流動模型里。
長度為L的井筒內流體與地層間的熱交換可由式(5)來計算:
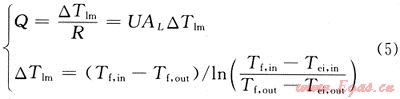
圖1顯示了井筒流體與地層間熱交換最全面的熱阻構成。總傳熱系數U或熱阻R,由6項串聯組成:①井筒內流體的對流換熱;②井筒壁的熱傳導;③井筒與套管間環形空間套筒液的對流換熱;④套筒壁的熱傳導;⑤混凝土的熱傳導;⑥地層的熱阻。
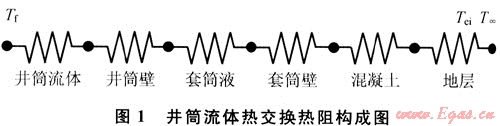
該熱交換的總傳熱系數和熱阻可由式(6)計算:
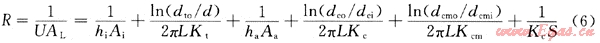
式中:最后一項是地層的熱阻,井筒的敷設系數S按埋地管道計算:
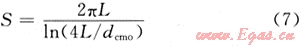
不是所有的熱交換都包含上述6個過程,如海洋中井筒的某個部分可能暴露在海水中。
對流換熱對總傳熱系數有大的影響,有很多計算對流換熱系數的關系式,它們基于流體和流動的性質,幾乎都可以表示成下述無量綱形式:
Nu=f(Re,Pr) (8)
式中:Nu是Nusselt數,是無量綱的傳熱系數;Re是雷諾數;Pr是Prandtl數。Dittus-Boelter關系式是對流傳熱系數關系式的一種:
Nu=0.023Re0.8Prn (9)
對井筒流體加熱,式中n取0.4,冷卻則取0.3。Dittus-BoeIter關系式適用于5000<Re<500000和Prandtl數為0.6~1000的情形。還有很多其他的關系式可供選擇,筆者綜合了多種關系式來處理大范圍的雷諾數和Prandtl數。
4 模型求解
有很多方法可用來求解井筒流動模型的微分方程組,筆者采用隱式法,它對求解方向無限制,同時可保證解的整體收斂性。
將整個井筒用步長△x分成n等分,對每段用中心差商代替其微分,式(3)就簡化為差分方程組,對整個井筒流動來說,模型轉化為一個非線性代數方程組:
fi(vf,Pj,Tj)=0,j=0,1,…,n;i=1,2,…,3n (10)
式中:下標i指方程,j指變量,n是井筒的分段數目。
式(10)描述了一個非線性代數方程組,對分為n段的井筒流動模型來說,共有3n個方程和3(n+1)個待求變量。因此還必須根據井筒流動分析的目的,給定3個定解邊界條件,如給定流量、井底壓力和溫度,即可確定井口需要注入的壓力和溫度。
解非線性方程組需要一個迭代過程和迭代初始值,且該初始值要足夠準確以保證收斂。當流體特性復雜或有相態變化時,解的收斂就是一個挑戰。筆者先用簡單模型確定2個端點的壓力和溫度初值,再沿井筒線性分布各段的相應初值。
此外,這里采用擬牛頓法求解這個非線性代數方程組,它既能很快收斂,又允許較寬的初值范圍。
5 應用實例和討論
基于上述理論和方法,開發了井筒酸氣流動和相態分布分析軟件GLEWpro。下面給出它的應用實例和討論。
5.1 伊朗Kharg島
此例計算伊朗Kharg島酸氣回注系統井口壓力和井筒流動分布[5]。該井為垂直152.4mm管4150m深,最大預期回注流量為2548×103m3/d。表1給出酸氣的構成。估計的沙面為62.2MPa和120℃,井口回注溫度是40℃,根據上述方法計算的總傳熱系數為1.91W/m2·K,其中地層的熱阻占總熱阻的97.66%,主導井筒流體與地層間的熱交換。
表1 Kharg酸氣組成表
|
組分
|
摩爾分數/%
|
組分
|
摩爾分數/%
|
|
H2O
|
0.3283
|
iC4
|
0.0516
|
|
H2S
|
52.7018
|
nC4
|
0.1094
|
|
CO2
|
45.5745
|
iC5
|
0.0547
|
|
C1
|
0.4253
|
nC5
|
0.0599
|
|
C2
|
0.4021
|
C6+
|
0.0281
|
|
C3
|
0.2642
|
|
|
在整個井筒酸氣都處于液相,計算的井口回注壓力為26.39MPa(263.9bar),井底流體的溫度是40.9℃。沿井筒的壓力、溫度和密度分布顯示在圖2。
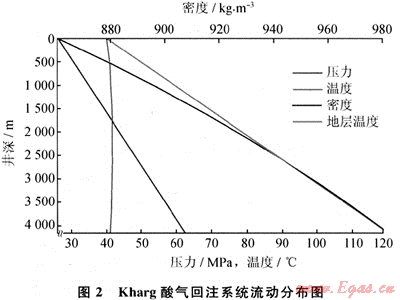
井口壓力的計算受許多設計方案和運行條件影響,敏感分析是解決矛盾的最好途徑,表2給出了一個簡單敏感分析的結果,它揭示了不同設置和條件對回注壓力的影響。通過比較我們可以看到,更改回注流量對回注壓力的影響很小。
表2 Kharg系統回注壓力敏度分析表
|
項目
|
初始值
|
新設置
|
新結果
|
|
|
井口壓力/MPa
|
井底結果/℃
|
|||
|
井口溫度/℃
|
40
|
20
|
24.08
|
18.5
|
|
井底溫度/℃
|
120
|
100
|
26.38
|
|
|
流量/103m3·d-1
|
2548
|
1274
|
25.17
|
43.6
|
|
井底壓力/MPa
|
62.2
|
52.0
|
18.07
|
45.2
|
|
井筒外徑/mm
|
168.275
|
127
|
34.07
|
39.4
|
5.2 加拿大Alberta省Anderson West Culp
該例計算Anderson West Culp酸氣回注系統井筒底部壓力和井筒流動分布[6]。該井筒為Ø60.325mm管(ID=50.673mm,壁厚4.826mm)垂直1943m深,酸氣組成H2S為60%,CO2為39%,C1為1%。在回注流量為0.6MMSCFD和井口在5.8MPa和3℃的情況下,GLEWpro估計井壓力是21.04MPa,這與本文參考文獻[6]測量的20.2MPa非常接近。圖3顯示了沿井筒的壓力、溫度和密度分布。
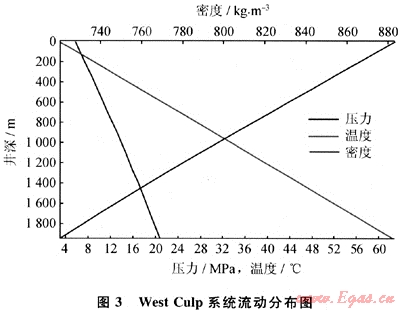
5.3 加拿大Alberta省Anderson North Normandville
回注井筒是1858m深的Ø60.325mm管[6]。酸氣由67%的H2S、32%的CO2和1%的CH4組成,需要注入0.08MMSCFD的酸氣到19.014MPa和60℃的地層中,井口流體溫度是3℃。
井筒的總傳熱系數為3W/m2·K,計算的井口壓力是4.19MPa和井底流體溫度55.3℃,與本文參考文獻E6]中所報告的4.38MPa非常吻合。圖4顯示了壓力、溫度和密度的分布。
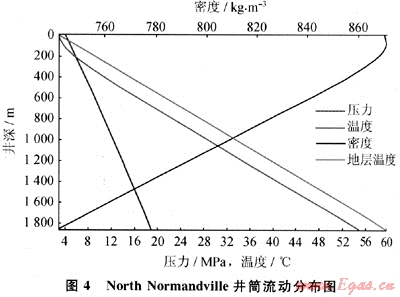
5.4 加拿大Alberta省Anderson Puskwaskau
該系統要將0.106 MMSCFD的酸氣通過Ø60.325mm英寸的井筒注入2670m深的地層,所注入的酸氣組成隨時間略有不同,約為45%的H2S、51%的CO2和4%的CH4。井底壓力和溫度分別是29.5MPa和82℃[6]。
這里進行了一系列計算,以確定回注溫度對回注壓力的影響。圖5顯示了井口回注溫度從0℃到30℃變化時所需的井口回注壓力。
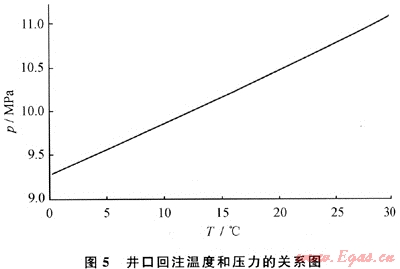
5.5 加拿大Alberta省Chevron,Acheson
Acheson回注系統的壓力相對較低,其地層壓力和溫度約為2400kPa和49℃,井深為1192m。酸氣由90.72%的H2S、8.25%的CO2和1.03%的甲烷構成[7]。本文參考文獻[7]未提及井筒的尺寸,這里假定為Ø60.325mm管。
在用GLEWpro計算這種情況下的回注壓力時,考慮了3種計算方案:①從井口3℃到井底49℃的線性溫度分布;②等溫分布(3℃);③自井口到井底環境溫度線性分布,酸氣與環境有熱交換,總傳熱系數假定為20W/m·K。表3列出了3種方案的結果。
表3 不同方案的井口回注壓力表
|
項目
|
方案1
|
方案2
|
方案3
|
|
井口壓力/MPa
|
2.06
|
1.99
|
2.05
|
|
井底溫度/℃
|
49.30
|
3.00
|
45.90
|
在這種情況下,由于壓力較低,在整個井筒酸氣為氣相,回注壓力受溫度分布的影響不大。
作為比較,實際系統的井口壓力約為2.5MPa,這比所計算的3個回注壓力都高出不少。
5.6 加拿大Alberta省Chevron,West Pembina
回注井深2810m,井筒為Ø60.325mm管,井底壓力和溫度是26.9MPa和98℃,要注入37℃的8.0×103m3/a的酸氣混合物(3.24%的H2O、55.93%的H2S、38.35%的CO2、1.88%的CH4及0.6%的C2H6)[7]。GLEWpro認為井筒流動為液體,需要的回注壓力是6.65MPa,這與本文參考文獻[7]的7.1MPa比較接近。
5.7 加拿大Alberta省Chevron,Bigoray
回注井深2396m,井筒為Ø60.325mm管,井底壓力和溫度是20.4MPa和61℃,要注入5℃的7.1×103m3/d的酸氣混合物(9.2%的H2S、89.8%的C02和1%的CH4)。GLEWpro估計的回注壓力是3.91MPa,與本文參考文獻[7]所報告的4.056MPa非常接近。本文參考文獻[7]指出在距井口239.4m左右流體從多相轉變為完全液相,GLEWpro顯示這個轉變發生在250m處,流動和相態分布見圖6。
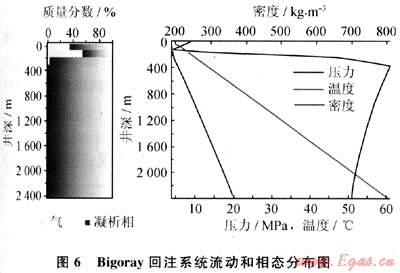
5.8 加拿大Alberta省PanCanadian Wayne-Rosedale
回注井深1926.5m,井筒為Ø60.325mm管,酸氣(20%的H2S和80%的CO2)的回注流量為21×103m3/d,井底壓力和溫度為20MPa和65℃[8]。當回注溫度20℃時,所需的井口壓力是6.4MPa,與本文參考文獻[8]所報告的實際回注壓力6.5MPa非常接近。
5.9 加拿大Alberta省Pouce Coupe
Pouce Coupe回注井深1452m,井筒為Ø60.325mm管,2003年6月測量的井底壓力為23 157kPa、溫度為74℃。2005年4月5日,23.95×103m3/a的酸氣(組成見表4)以井口壓力8.3 MPa和溫度3℃被注入地層。若取總傳熱系數為3W/m3·K,GLEWpro軟件估計的井底壓力是21.25MPa,井底流體溫度是30.3℃。
表4 Pouce Coupe酸氣組成表
|
組分
|
摩爾分數/%
|
組分
|
摩爾分數/%
|
|
H2S
|
45.600
|
iC4
|
0.005
|
|
C02
|
53.900
|
nC4
|
0.008
|
|
C1
|
0.460
|
iC5
|
0.010
|
|
C2
|
0.007
|
nC5
|
0.010
|
5.10 井噴
酸氣回注系統設計中另一個重要的考慮是如何防止和處理災難性事故,如井噴。設計時工程師必須要能夠估計此時酸氣的流量,以制訂相應的緊急應急方案。
以上述West Pembina系統為例,如果流動處于開口狀態,即井口壓力為101.325kPa,通過GLEWpro分析可知,該井噴流動在井口達到臨界狀態,其壓力為521kPa、速度為290m/s、流量為23.62×103m3/a,在300m深時流動從液相轉變為氣相,如圖7所示。
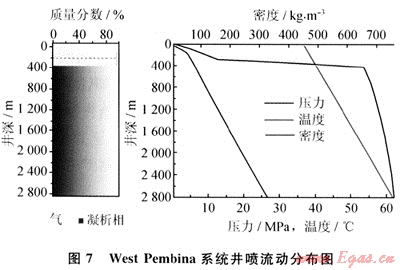
6 結論
在設計和操作成本低廉、環保的酸氣回注系統時,越來越重視井筒的流動和相態分布,而一個全面的井筒流動和相態分布水力和熱力模型,是正確分析在不同井筒結構、操作條件和要求以及酸氣熱力學性質情況下井筒內流動和相態分布的基本保證。
由于井筒內流體與周圍地層的熱交換以及環境溫度隨井深不斷增加,井筒內流體溫度將隨井深顯著變化。合適的熱力分析是井筒流動精確分析的必然需要。
從應用實例和討論中可以看到,GLEWpro軟件的結果與文獻中的略有不同,這是由參數、設置和所選方法的差異造成的。在井筒內有相態變化時,需要更多的迭代過程。
符號說明
A為井筒內截面積,m2;Aa為套管內表面積,m2;Ai為井筒內表面積,m2;AL為熱交換面積,m2;d為井筒內徑,m;dci為套管內徑,m;dcmi為混凝土層內徑,m;dcmo為混凝土層外徑,m;dco為套管外徑,m;dto為井筒外徑,m;f為達西摩阻系數;hi為井筒液對流換熱系數,W/m2·K;ha為套管液對流換熱系數,W/m2·K;g為重力加速度,m/s2;K為井筒液熱導率,W/m·K;Kc為套管熱導率,W/m·K;Kcm為混凝土熱導率,W/m·K;Ke為地層土壤熱導率,W/m·K;Kt為井筒熱導率,W/m·K;MFi為酸氣i組分的摩爾分數;MW為酸氣i組分的摩爾質量,kg/kmol;pj為在xj處的壓力,Pa;Q為傳熱量,J/s;t為時間,s;Tj為在xj處的溫度,K;v為速度,m/s;vj為在xj處的速度,m/s;x為沿井筒坐標,m;yi為酸氣i組分的質量分數;z為高程,m;△T1m為對數平均溫度差,K;μ為流體黏度,Pa·s;ρ為流體密度,kg/m3;文中下標符號cm指混凝土,e指地層土壤,ei指地層土壤的初始狀況,f指流體,i指內部,in指管段的初始位置,m指混合物,o指外部,out指管段的結束位置,t指井筒。
參考文獻
[1] CARROLL J J,SHOUXI WANG,湯林.酸氣回注:酸氣處理的另一途徑[J].天然氣工業,2009,29(10):96-100.
[2] 吳海浩,孫濱斌,孫宇,等.重組分對天然氣相態特征的影響[J].天然氣工業,2008,28(11):99-102.
[3] CARROLL J J. The water content of acid gas and sour gas from 100°to 220℉ and pressures to 1O000 psia[C]∥81st Annual GPA Convention. Dallas:TX,2002.
[4] WANG S,CARROLL J J. Model calculates Acid-Gas injection profiles[J].Oil & Gas Journal,2006,33(9):4.
[5] RAHIMI N,GRIFFIN P J. Potential for acid gas injection at Kharg Island[C].Doha:SOGAT,2004.
[6] MADDOCKS J R,WHITESIDE D.Acid gas injection:an operator’s perspective[C].Doha:SOGAT,2004.
[7] BOSCH N. Acid gas injection-a decade of operating history in western Canada[C].Calgary:CGPSA,2002.
[8] HO K T,MCMULLEN J,BOYLE P,et al. Subsurface acid gas disposal scheme in Wayne-Rosedale[C]∥SPE 35848.Calgary:SPE,1996.
(本文作者:王壽喜1 John J.Carroll1 湯林2 1.Gas Liquids Engineering Ltd.;2.中國石油勘探與生產分公司)
贊 賞 分享
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助
- 注解:本資料由會員及群友提供僅供閱讀交流學習,不得用于商業用途!
